Задача 80571 Нужно решить задачу ДУ номер 3 и 4...
Условие
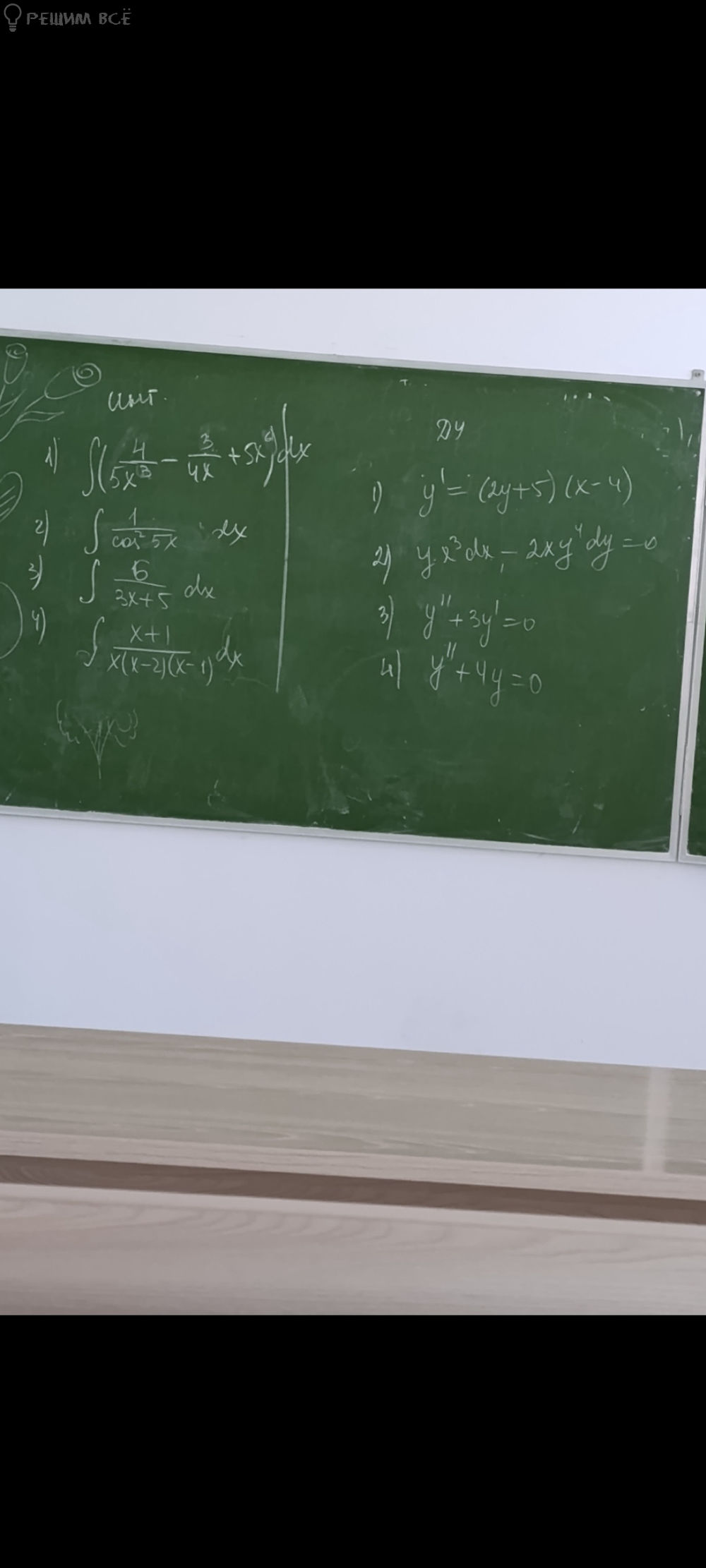
27
Решение
★
Линейное однородное уравнение 2 порядка с постоянными коэффициентами.
Характеристическое уравнение:
k^2 + 3k = 0
k(k + 3) = 0
k1 = 0, k2 = -3
Если корни действительные, то решение уравнения:
[m]y = C1e^{k1x} + C2e^{k2x}[/m]
[m]y = C1e^{0x} + C2e^{-3x}[/m]
[m]y = C1 + C2e^{-3x}[/m]
4) y'' + 4y = 0
Линейное однородное уравнение 2 порядка с постоянными коэффициентами.
Характеристическое уравнение:
k^2 + 4 = 0
k1 = -2i; k2 = 2i
Если корни комплексные k = a ± bi, то решение уравнения:
[m]y = e^{a}(C1 \cos bx + C2 \sin bx)[/m]
У нас k = 0 ± 2i, то есть a = 0, b = 2, поэтому:
[m]y = e^{0}(C1 \cos 2x + C2 \sin 2x)[/m]
[m]y = C1 \cos 2x + C2 \sin 2x[/m]