Задача 80570 Нужно решить задачу ДУ номер 2...
Условие
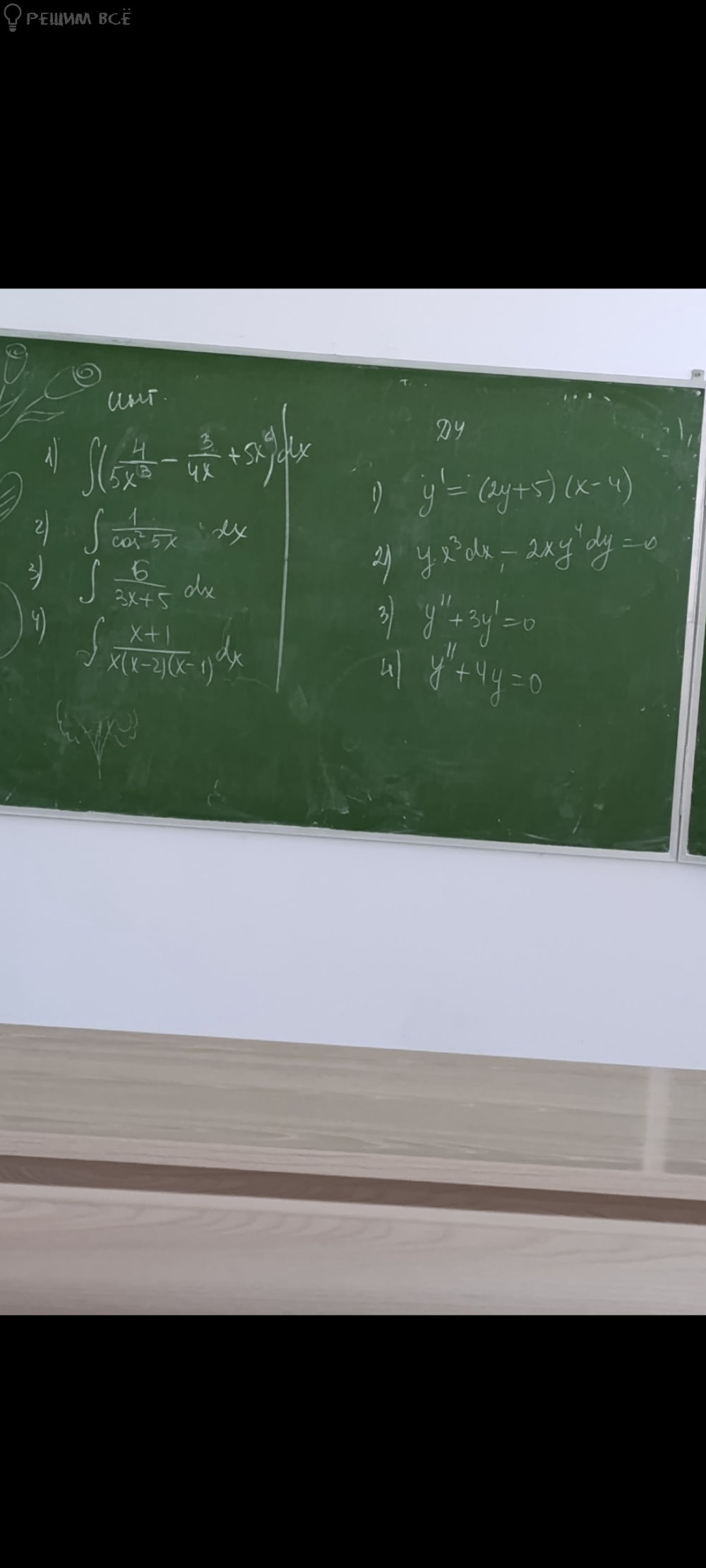
20
Решение
★
Уравнение с разделяющимися переменными, как и 1)
2xy^4 dy = yx^3 dx
Делим на xy левую и правую части:
2y^3 dy = x^2 dx
Берем интегралы от левой и правой частей:
[m]\int 2y^3 dy = \int x^2 dx[/m]
[m]\frac{2y^4}{4} = \frac{x^3}{3} + \frac{C}{2}[/m]
Как и в 1), здесь удобнее взять C/2 вместо C.
[m]\frac{y^4}{2} = \frac{x^3}{3} + \frac{C}{2}[/m]
Умножаем левую и правую части на 6:
3y^4 = 2x^3 + 3C
Можно оставить в этом неявном виде, а можно выделить y:
y^4 = 2x^3/3 + C
[m]y = ± \sqrt[4]{\frac{2x^3}{3} + C}[/m]
Но я бы лучше оставил в неявном виде.