Задача 80569 Нужно решить задачу ДУ номер 1...
Условие
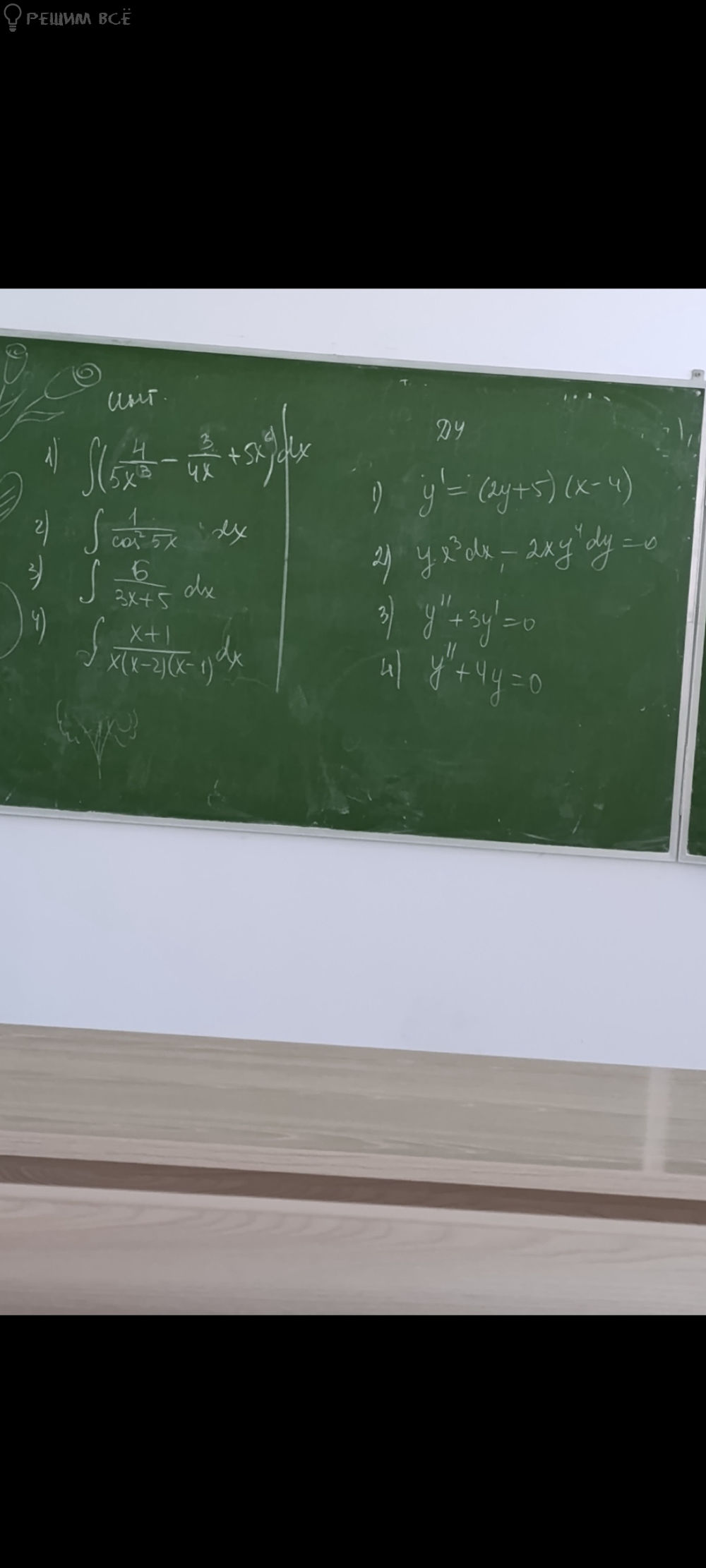
11
Решение
★
Это уравнение с разделяющимися переменными.
[m]\frac{dy}{dx} = (2y+5)(x-4)[/m]
[m]\frac{dy}{2y+5} = (x - 4)dx[/m]
Берем интегралы от левой и правой части:
[m]\int \frac{dy}{2y+5} = \int (x - 4)dx[/m]
[m]\frac{1}{2} \cdot \ln |2y+5| = \frac{x^2}{2} - 4x + \frac{C}{2}[/m]
Я написал C/2, а не C, потому что здесь так удобнее.
Умножаем на 2 обе части:
[m]\ln |2y+5| = x^2 - 8x + C[/m]
Переходим от логарифма к y:
[m]\large 2y + 5 = e^{x^2 - 8x + C}[/m]
[m]\large y = \frac{e^{x^2 - 8x + C} - 5}{2}[/m]