Задача 80561 нужно решить 7 номер методом гаусса...
Условие
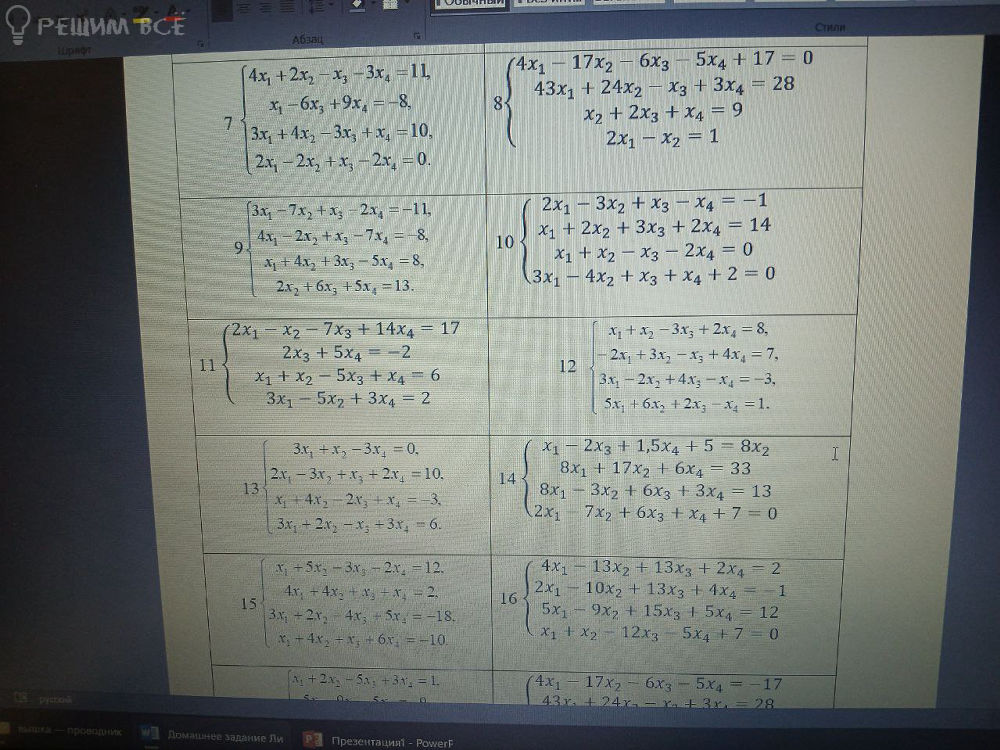
Решение
{ x1 - 6x3 + 9x4 = -8
{ 3x1 + 4x2 - 3x3 + x4 = 10
{ 2x1 - 2x2 + x3 - 2x4 = 0
Строим расширенную матрицу:
[m]\begin{pmatrix}
4 & 2 & -1 & -3 & | & 11 \\
1 & 0 & -6 & 9 & | & -8 \\
3 & 4 & -3 & 1 & | & 10 \\
2 & -2 & 1 & -2 & | & 0 \\
\end{pmatrix}[/m]
Поменяем местами строки:
[m]\begin{pmatrix}
1 & 0 & -6 & 9 & | & -8 \\
2 & -2 & 1 & -2 & | & 0 \\
3 & 4 & -3 & 1 & | & 10 \\
4 & 2 & -1 & -3 & | & 11 \\
\end{pmatrix}[/m]
1 строку умножаем на -2 и складываем со 2 строкой.
1 строку умножаем на -3 и складываем с 3 строкой.
1 строку умножаем на -4 и складываем с 4 строкой.
[m]\begin{pmatrix}
1 & 0 & -6 & 9 & | & -8 \\
0 & -2 & 13 & -20 & | & 16 \\
0 & 4 & 15 & -26 & | & 34 \\
0 & 2 & 23 & -39 & | & 43 \\
\end{pmatrix}[/m]
Умножаем 2 строку на 2 и складываем с 3 строкой.
Складываем 2 и 4 строки.
[m]\begin{pmatrix}
1 & 0 & -6 & 9 & | & -8 \\
0 & -2 & 13 & -20 & | & 16 \\
0 & 0 & 41 & -66 & | & 66 \\
0 & 0 & 36 & -59 & | & 59 \\
\end{pmatrix}[/m]
Умножаем 3 строку на 36, а 4 строку на -41, и складываем их.
[m]\begin{pmatrix}
1 & 0 & -6 & 9 & | & -8 \\
0 & -2 & 13 & -20 & | & 16 \\
0 & 0 & 41 & -66 & | & 66 \\
0 & 0 & 0 & 43 & | & -43 \\
\end{pmatrix}[/m]
Возвращаемся к системе:
{ x1 + 0x2 - 6x3 + 9x4 = -8
{ 0x1 - 2x2 + 13x3 - 20x4 = 16
{ 0x1 + 0x2 + 41x3 - 66x4 = 66
{ 0x1 + 0x2 + 0x3 + 43x4 = -43
Из 4 уравнения:
[b]x4 = -1[/b]
Подставляем в 3 уравнение:
41x3 + 66 = 66
[b]x3 = 0[/b]
Подставляем во 2 уравнение:
-2x2 + 0 + 20 = 16
-2x2 = -4
[b]x2 = 2[/b]
Подставляем в 1 уравнение:
x1 + 0 - 0 - 9 = -8
[b]x1 = 1[/b]
Ответ: (1; 2; 0; -1)