Задача 80555 MKLN — ромб со стороной n. Стороны KM и...
Условие
Решение
Сторона |MK| = |KL| = |LN| = |NM| = m
В задании написано m, а в ответах везде n.
Где-то опечатка, скорее всего в задании.
Угол KMN = 120°
Найти:
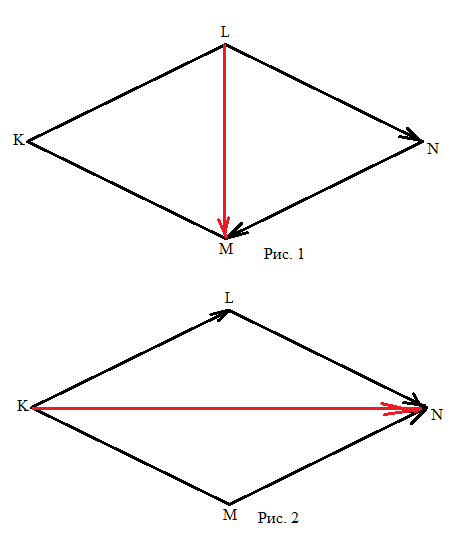
1) |LN + NM| = |LM|
Смотри Рис. 1. Вектор LM обозначен красным.
Так как KMN = 120°, то LNM = 180° - 120° = 60°
Треугольник LMN - равносторонний, поэтому
|LN + NM| = |LM| = |LN| = n
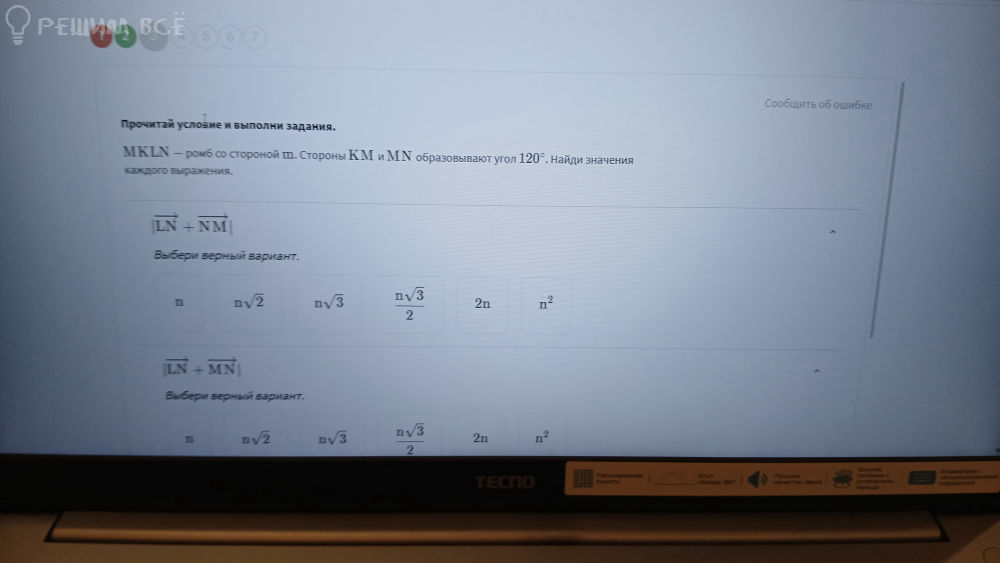
2) |LN + MN|
Угол KMN = KLN = 120°
Вектор MN = KL, он получается параллельным переносом.
|LN + MN| = |LN + KL| = |KL + LN| = |KN|
Смотри Рис. 2. Вектор KN обозначен красным.
По теореме косинусов:
|KM|^2 = |KL|^2 + |LM|^2 - 2*|KL|*|LM|*cos KLN
|KM|^2 = n^2 + n^2 - 2*n*n*cos 120° = 2n^2 - 2n^2*(-1/2) =
= 2n^2 + n^2 = 3n^2
|LN + MN| = |KN| = n*sqrt(3)