Задача 80553 Нужно решить задачу интеграл , номер 3 и...
Условие
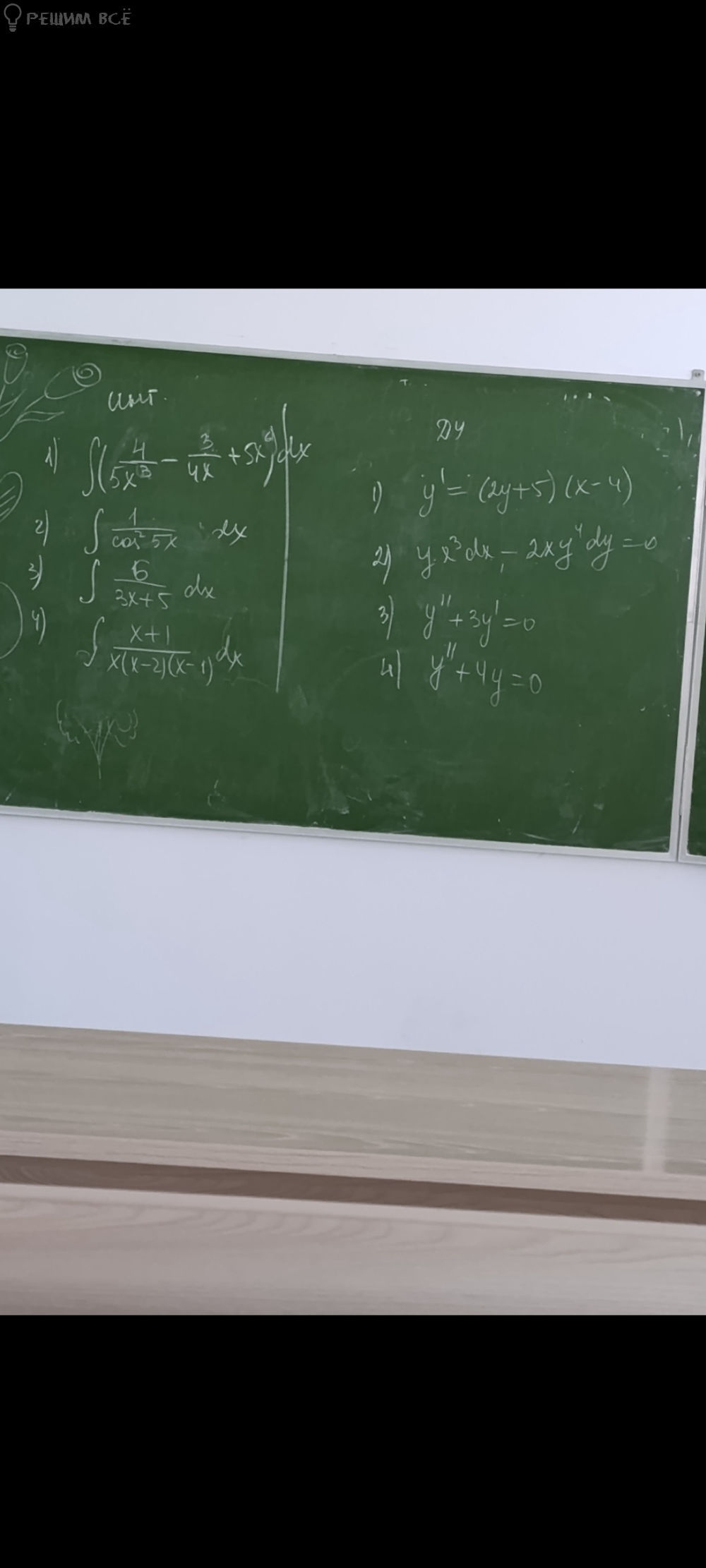
Решение
4) [m]\int \frac{x+1}{x(x-2)(x-1)} dx[/m]
Метод неопределенных коэффициентов.
Разложим дробь на сумму дробей:
[m]\frac{x+1}{x(x-2)(x-1)} = \frac{A1}{x} + \frac{A2}{x-2} + \frac{A3}{x-1} = \frac{A1(x-2)(x-1) + A2x(x-1) + A3x(x-2)}{x(x-2)(x-1)} =[/m]
[m]= \frac{A1(x^2-3x+2) + A2(x^2-x) + A3(x^2-2x)}{x(x-2)(x-1)} = [/m]
[m]= \frac{(A1+A2+A3)x^2 + (-3A1 -A2 -2A3)x +2A1}{x(x-2)(x-1)}[/m]
Составляем систему по коэффициентам при степенях x:
{ A1 + A2 + A3 = 0 (коэффициент при x^2)
{ -3A1 - A2 - 2A3 = 1 (коэффициент при x)
{ -2A3 = 1 (свободный член)
Из 3 уравнения: [b]A3 = -1/2[/b]
Подставляем в 1 и 2 уравнения:
{ A1 + A2 - 1/2 = 0
{ -3A1 - A2 + 1 = 1
Решаем:
{ A1 + A2 = 1/2
{ -3A1 - A2 = 0
Складываем уравнения:
-2A1 = 1/2
[b]A1 = -1/4[/b]
A2 = 1/2 - A1 = 1/2 + 1/4
[b]A2 = 3/4[/b]
Возвращаемся к интегралу:
[m]\int \frac{x+1}{x(x-2)(x-1)} dx = \int (\frac{A1}{x} + \frac{A2}{x-2} + \frac{A3}{x-1})dx = [/m]
[m]= \int (\frac{-1}{4x} + \frac{3}{4(x-2)} + \frac{-1}{2(x-1)}) dx =[/m]
[m]= -\frac{1}{4} \cdot \ln |x| + \frac{3}{4} \cdot \ln |x-2| - \frac{1}{2} \cdot \ln |x-1| + C[/m]