Задача 80552 ...
Условие
Задана линия своим уравнением в полярной системе координат. Необходимо:
1) определить точки, лежащие на линии, придавая φ значения через
промежуток, равный π/8, начиная от φ = 0 и до φ = 2π; 2) построить линию,
соединив полученные точки; 3) найти уравнение этой линии в декартовой
системе координат.
p=3 (1-cos 4 φ )
Решение
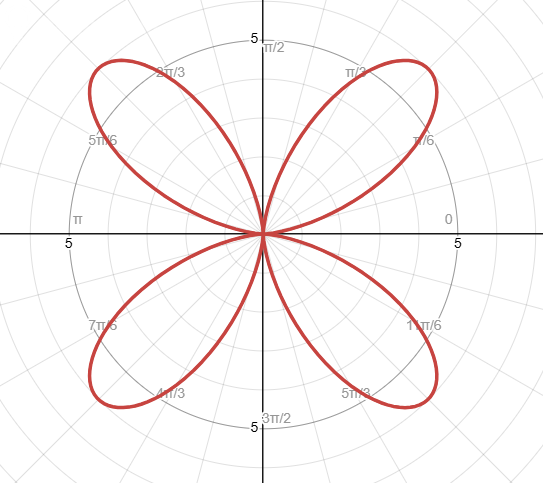
График я построил, смотрите Рисунок 1.
Таблица точек через π/8 от 0 до 2π = 16π/8
ρ(0) = 3(1 - cos 4*0) = 3*(1 - cos 0) = 3(1 - 1) = 0
ρ(π/8) = 3(1 - cos 4*π/8) = 3*(1 - cos π/2) = 3(1 - 0) = 3
ρ(2π/8) = 3(1 - cos 4*2π/8) = 3*(1 - cos π) = 3(1 + 1) = 6
ρ(3π/8) = 3(1 - cos 4*3π/8) = 3*(1 - cos 3π/2) = 3(1 - 0) = 3
ρ(4π/8) = 3(1 - cos 4*4π/8) = 3*(1 - cos 2π) = 3(1 - 1) = 0
ρ(5π/8) = 3(1 - cos 4*5π/8) = 3*(1 - cos 5π/2) = 3(1 - 0) = 3
ρ(6π/8) = 3(1 - cos 4*6π/8) = 3*(1 - cos 3π) = 3(1 + 1) = 6
ρ(7π/8) = 3(1 - cos 4*7π/8) = 3*(1 - cos 7π/2) = 3(1 - 0) = 3
ρ(8π/8) = 3(1 - cos 4*8π/8) = 3*(1 - cos 4π) = 3(1 - 1) = 0
ρ(9π/8) = 3(1 - cos 4*9π/8) = 3*(1 - cos 9π/2) = 3(1 - 0) = 3
ρ(10π/8) = 3(1 - cos 4*10π/8) = 3*(1 - cos 5π) = 3(1 + 1) = 6
ρ(11π/8) = 3(1 - cos 4*11π/8) = 3*(1 - cos 11π/2) = 3(1 - 0) = 3
ρ(12π/8) = 3(1 - cos 4*12π/8) = 3*(1 - cos 6π) = 3(1 - 1) = 0
ρ(13π/8) = 3(1 - cos 4*13π/8) = 3*(1 - cos 13π/2) = 3(1 - 0) = 3
ρ(14π/8) = 3(1 - cos 4*14π/8) = 3*(1 - cos 7π) = 3(1 + 1) = 6
ρ(15π/8) = 3(1 - cos 4*15π/8) = 3*(1 - cos 15π/2) = 3(1 - 0) = 3
ρ(16π/8) = 3(1 - cos 4*16π/8) = 3*(1 - cos 8π) = 3(1 - 1) = 0
Чтобы перевести его в декартову систему, нужно воспользоваться формулами перехода:
{ x = ρ*cos φ
{ y = ρ*sin φ
Нам нужно выразить отсюда ρ и φ.
{ x^2 = ρ^2*cos^2 φ
{ y^2 = ρ^2*sin^2 φ
x^2 + y^2 = ρ^2*(cos^2 φ + sin^2 φ) = ρ^2
ρ = sqrt(x^2 + y^2)
cos φ = x/ρ = x/sqrt(x^2 + y^2)
sin φ = y/ρ = y/sqrt(x^2 + y^2)
Выразим cos 4φ через cos φ и sin φ.
cos 4φ = 1 - 2sin^2 2φ = 1 - 2*(2sin φ*cos φ)^2 = 1 - 8sin^2 φ*cos^2 φ
[m]\cos 4φ = 1 - 8 \cdot \frac{y^2}{x^2+y^2} \cdot \frac{x^2}{x^2+y^2} = 1 - \frac{8x^2y^2}{(x^2+y^2)^2}[/m]
Подставляем это в уравнение:
[m]\sqrt{x^2 + y^2} = 3(1 - (1 - \frac{8x^2y^2}{(x^2+y^2)^2})) = 3(1 - 1 + \frac{8x^2y^2}{(x^2+y^2)^2})[/m]
[m]\sqrt{x^2 + y^2} = \frac{24x^2y^2}{(x^2+y^2)^2}[/m]
Умножаем на (x^2+y^2)^2:
[m](x^2+y^2)^{2,5} = 24x^2y^2[/m]
Получилось уравнение в неявном виде, получить из него уравнение в прямом виде: y = f(x) - может быть, и можно, но я не знаю, как.
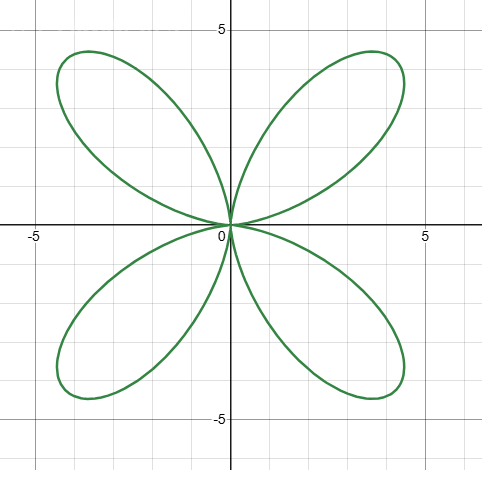
На Рисунке 2 показан этот же график в декартовых координатах.
Как видите, кривая точно такая же. Это значит, что решение верное.