Задача 80547 Решите примеры. Найдите пределы, не...
Условие
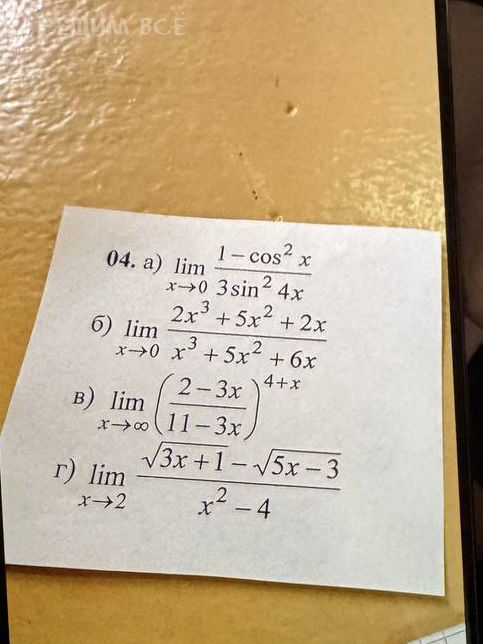
Решение
1 Замечательный предел:
[m]\lim \limits_{z \to 0} \frac{\sin z}{z} = 1[/m]
Поэтому преобразуем наш предел так:
[m] \frac{1}{3} \cdot \lim \limits_{x \to 0} \frac{\sin^2 x}{x^2} \cdot \frac{(4x)^2}{\sin^2 4x} \cdot \frac{x^2}{(4x)^2} = [/m]
[m]= \frac{1}{3} \cdot 1 \cdot 1 \cdot \frac{x^2}{16x^2} = \frac{1}{3} \cdot \frac{1}{16} = \frac{1}{48}[/m]
б) [m]\lim \limits_{x \to 0} \frac{2x^3+5x^2+2x}{x^3+5x^2+6x} = \lim \limits_{x \to 0} \frac{2x^2+5x+2}{x^2+5x+6} = \frac{0+0+2}{0+0+6} = \frac{1}{3}[/m]
Сократили x, потом подставили 0 вместо x.
в) [m]\lim \limits_{x \to \infty} \bigg ( \frac{2-3x}{11-3x} \bigg )^{4+x} = \lim \limits_{x \to \infty} \bigg ( \frac{3x-2}{3x-11} \bigg )^{x+4}[/m]
Можно поменять знаки одновременно в числителе и знаменателе,
от этого значение дроби не изменится.
[m]\lim \limits_{x \to \infty} \bigg ( \frac{3x-11+9}{3x-11} \bigg )^{x+4} = \lim \limits_{x \to \infty} \bigg (1 + \frac{9}{3x-11} \bigg )^{x+4}[/m]
Теперь нужно поставить в показатель степени то же выражение,
которое стоит в знаменателе. Умножим и разделим на него.
[m]\lim \limits_{x \to \infty} \bigg ( \frac{3x-11+9}{3x-11} \bigg )^{x+4} = \lim \limits_{x \to \infty} \bigg (1 + \frac{9}{3x-11} \bigg )^{(3x-11) \cdot \frac{x+4}{3x-11}}[/m]
2 Замечательный предел в общем виде:
[m]\lim \limits_{z \to \infty} \bigg (1 + \frac{k}{z} \bigg )^{zn} = e^{kn}[/m]
В нашем случае: k = 9, z = 3x - 11, n = (x+4)/(3x-11)
[m]\lim \limits_{x \to \infty} \bigg (1 + \frac{9}{3x-11} \bigg )^{(3x-11) \cdot \frac{x+4}{3x-11}} = \lim \limits_{x \to \infty} e^{9 \cdot \frac{x+4}{3x-11}} = [/m]
[m]= e^{9 \cdot \lim \limits_{x \to \infty} \frac{x+4}{3x-11}} = e^{\frac{9}{3}} = e^3[/m]
г) [m]\lim \limits_{x \to 2} \frac{\sqrt{3x+1} - \sqrt{5x-3}}{x^2-4}[/m]
Числитель умножаем и делим на сопряжённое (сумму корней), знаменатель раскладываем на скобки как разность квадратов.
[m]\lim \limits_{x \to 2} \frac{(\sqrt{3x+1} - \sqrt{5x-3})(\sqrt{3x+1} + \sqrt{5x-3})}{(x-2)(x+2)(\sqrt{3x+1} + \sqrt{5x-3})}[/m]
В числителе получилась разность квадратов.
[m]\lim \limits_{x \to 2} \frac{(3x+1) - (5x-3)}{(x-2)(x+2)(\sqrt{3x+1} + \sqrt{5x-3})} = \lim \limits_{x \to 2} \frac{4-2x}{(x-2)(x+2)(\sqrt{3x+1} + \sqrt{5x-3})} =[/m]
[m]=\lim \limits_{x \to 2} \frac{-2(x-2)}{(x-2)(x+2)(\sqrt{3x+1} + \sqrt{5x-3})} = \lim \limits_{x \to 2} \frac{-2}{(x+2)(\sqrt{3x+1} + \sqrt{5x-3})}[/m]
От проблемной скобки (x - 2) избавились, можно подставлять предел:
[m]\lim \limits_{x \to 2} \frac{-2}{(x+2)(\sqrt{3x+1} + \sqrt{5x-3})} = \frac{-2}{(2+2)(\sqrt{7} + \sqrt{7})} = -\frac{2}{4 \cdot 2\sqrt{7}} = -\frac{1}{4\sqrt{7}}[/m]