Задача 80539 Найти односторонние пределы, установить...
Условие
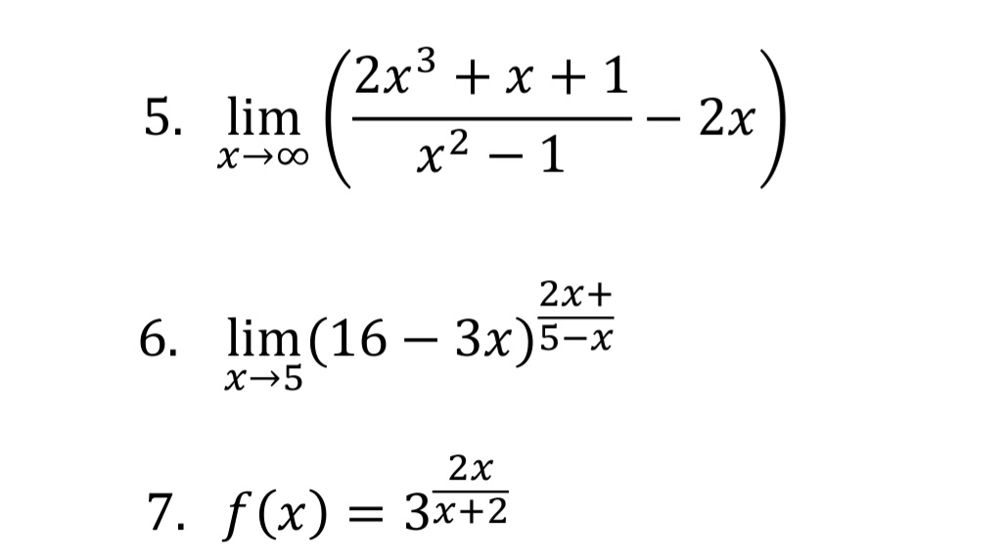
Решение
[m]=\lim \limits_{x \to \infty} \frac{2x^3+x+1 - 2x^3+2x}{x^2-1} =\lim \limits_{x \to \infty} \frac{3x+1}{x^2-1} =[/m]
[m]= \lim \limits_{x \to \infty} \frac{3/x + 1/x^2}{1 - 1/x^2} = \frac{0 + 0}{1 - 0}= 0[/m]
Ответ: 0
6) Непонятно, что в показателе
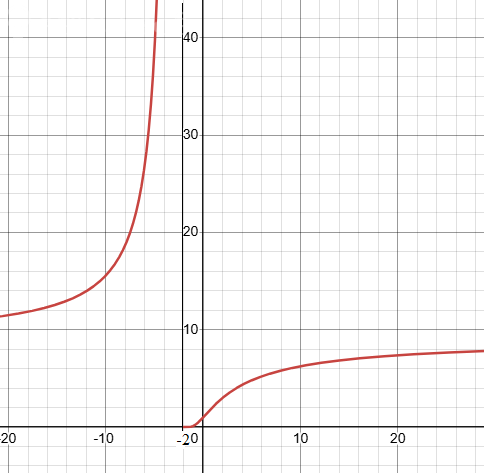
7) [m]\large f(x) = 3^{\frac{2x}{x+2}}[/m]
В точке x = -2 неустранимый разрыв 2 рода - уход в беско-нечность.
Предел слева:
[m]\large \lim \limits_{x \to -2-0} 3^{\frac{2x}{x+2}} = 3^{\frac{2(-2-0)}{-2-0+2}} = 3^{\frac{-4}{-0}} = 3^{\frac{4}{0}} = 3^{+\infty} = +\infty[/m]
Предел справа:
[m]\large \lim \limits_{x \to -2+0} 3^{\frac{2x}{x+2}} = 3^{\frac{2(-2+0)}{-2+0+2}} = 3^{\frac{-4}{+0}} = 3^{\frac{-4}{0}} = 3^{-\infty} =0[/m]
График на рисунке. Асимптота показана тонкой линией.