Задача 80538 помогите найти точки разрыва...
Условие
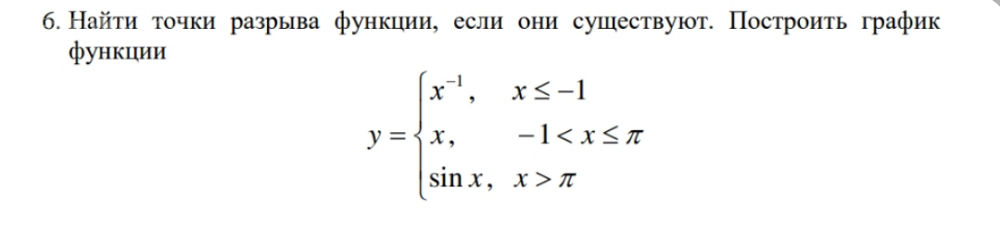
Решение
⎧ 1/x , x ≤ –1
y(x) = ⎨ x , –1 < x ≤ π
⎩ sinx , x > π
1. Область определения
D = (-∞,-1] ∪ (-1, π] ∪ (π,+∞).
2. Непрерывность на внутренних точках отрезков
• 1/x непрерывна при x<0 ⇒ при x≤–1 разрывов нет.
• x непрерывен на (-1, π] ⇒ разрывов нет.
• sinx непрерывна на (π,+∞) ⇒ разрывов нет.
3. Проверяем точки «стыка»
а) x = –1
– левосторонний предел: lim_{x→–1-} 1/x = –1;
– правосторонний предел: lim_{x→–1+} x = –1;
– значение функции: y(–1)=1/(–1)=–1.
Пределы равны и совпадают со значением ⇒ разрыва нет, функция непрерывна в –1.
б) x = π
– левосторонний предел: lim_{x→π-} x = π;
– правосторонний предел: lim_{x→π+} sinx = sinπ = 0;
Пределы разные ⇒ общего предела нет.
Значение функции y(π)=π (берётся из второй ветви).
⇒ в точке x = π разрыв 1-го рода (скачок).
Других «подозрительных» точек нет (x=0 в область определения не входит, поэтому по определению разрыва не рассматривается).
Итак
Точка (и тип) разрыва: x = π – разрыв первого рода (скачок).
Во всех остальных точках функция непрерывна.
4. Эскиз графика
• При x ≤ –1 – ветвь гиперболы y = 1/x (левая ветвь), точка (–1; –1) закрашена.
• На интервале (–1, π] – прямая y = x, точка (–1; –1) уже есть, точка (π; π) закрашена.
• При x > π – график y = sinx, начинается с незакрашенной точки (π; 0) и далее синусоидой.