Задача 80535 ...
Условие
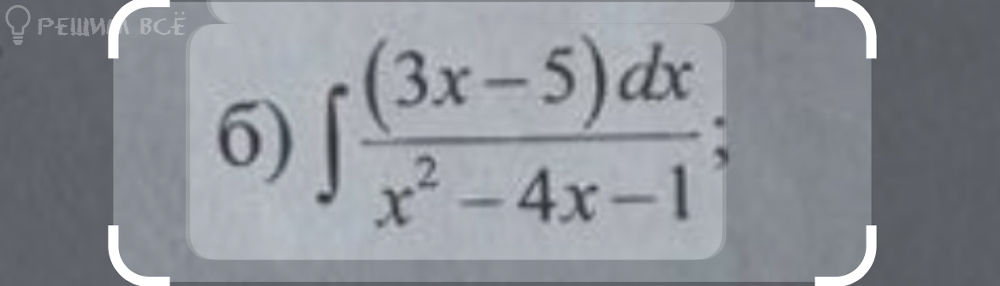
Решение
x^2 - 4x - 1 = 0
D/4 = (-2)^2 - 1(-1) = 4 + 1 = 5
x1 = 2 - sqrt(5); x2 = 2 + sqrt(5)
x^2 - 4x - 1 = (x - 2 + sqrt(5))(x - 2 - sqrt(5))
Решаем методом неопределенных коэффициентов
[m]\int \frac{3x-5}{x^2-4x-1} dx = \int \frac{3x-5}{(x - 2 + \sqrt{5})(x - 2 - \sqrt{5})} dx=[/m]
[m]= \int (\frac{A}{(x - 2 + \sqrt{5})} + \frac{B}{(x - 2 - \sqrt{5})}) dx[/m]
Складываем дроби:
[m]\frac{A}{(x - 2 + \sqrt{5})} + \frac{B}{(x - 2 - \sqrt{5})}= [/m]
[m]= \frac{A(x - 2 - \sqrt{5})}{(x - 2 + \sqrt{5})(x - 2 - \sqrt{5})} + \frac{B(x - 2 + \sqrt{5})}{(x - 2 + \sqrt{5})(x - 2 - \sqrt{5})} =[/m]
[m]= \frac{A(x - 2 - \sqrt{5}) + B(x - 2 + \sqrt{5})}{(x - 2 + \sqrt{5})(x - 2 - \sqrt{5})} = \frac{Ax - 2A - A\sqrt{5} + Bx - 2B + B\sqrt{5}}{(x - 2 + \sqrt{5})(x - 2 - \sqrt{5})}=[/m]
[m]= \frac{x(A + B) + (- 2A - A\sqrt{5} - 2B + B\sqrt{5})}{(x - 2 + \sqrt{5})(x - 2 - \sqrt{5})} = \frac{3x-5}{(x - 2 + \sqrt{5})(x - 2 - \sqrt{5})}[/m]
Составляем систему по коэффициентам:
{ A + B = 3
{ - 2A - A*sqrt(5) - 2B + B*sqrt(5) = -5
Решаем подстановкой:
{ B = 3 - A
{ - 2A - A*sqrt(5) - 2*(3 - A) + (3 - A)*sqrt(5) = -5
-2A - A*sqrt(5) - 6 + 2A + 3sqrt(5) - A*sqrt(5) = -5
3sqrt(5) - 6 + 5 = 2A*sqrt(5)
[m]A = \frac{3\sqrt{5} - 1}{2\sqrt{5}} = \frac{(3\sqrt{5} - 1) \cdot \sqrt{5}}{2 \cdot 5} = \frac{3 \cdot 5 - \sqrt{5}}{10}[/m]
[m]A = \frac{15 - \sqrt{5}}{10}[/m]
[m]B= 3 - A = 3 - \frac{15 - \sqrt{5}}{10} = \frac{15 + \sqrt{5}}{10}[/m]
Подставляем в интеграл. A и B я вынесу за интегралы:
[m]\int \frac{3x-5}{x^2-4x-1} dx = \frac{15 - \sqrt{5}}{10} \cdot \int \frac{dx}{(x - 2 + \sqrt{5})} + \frac{15 + \sqrt{5}}{10} \cdot \int \frac{dx}{(x - 2 - \sqrt{5})} =[/m]
[m]= \frac{15 - \sqrt{5}}{10} \cdot \ln |x - 2 + \sqrt{5}| + \frac{15 + \sqrt{5}}{10} \cdot \ln |x - 2 - \sqrt{5}| + C[/m]
Все решения
Замена переменной
[m]x-2=t[/m]
[m]x=t+2[/m]
[m]dx=(t+2)`dt[/m]
[m]dx=dt[/m]
[m] ∫ \frac{3x-5}{x^2-4x-1}dx= ∫ \frac{3x-5}{(x-2)^2-5}dx=[/m] замена переменной в интеграле
[m] ∫ \frac{3(t+2)-5}{t^2-5}dt=∫ \frac{3t+1}{t^2-5}dt=∫ \frac{3t}{t^2-5}dt+∫ \frac{1}{t^2-5}dt=[/m]
[m]=\frac{3}{2}∫ \frac{2t}{t^2-5}dt+∫ \frac{1}{t^2-5}dt=\frac{3}{2}ln|t^2-5|+\frac{1}{2\sqrt{5}}ln|\frac{t-\sqrt{5}}{t+\sqrt{5}}|+C[/m]
обратная замена ( переход к переменной х)
[m]=\frac{3}{2}ln|x^2-4x-1|+\frac{1}{2\sqrt{5}}ln|\frac{x-2-\sqrt{5}}{x+2+\sqrt{5}}|+C[/m]