Задача 80531 ...
Условие
Решение
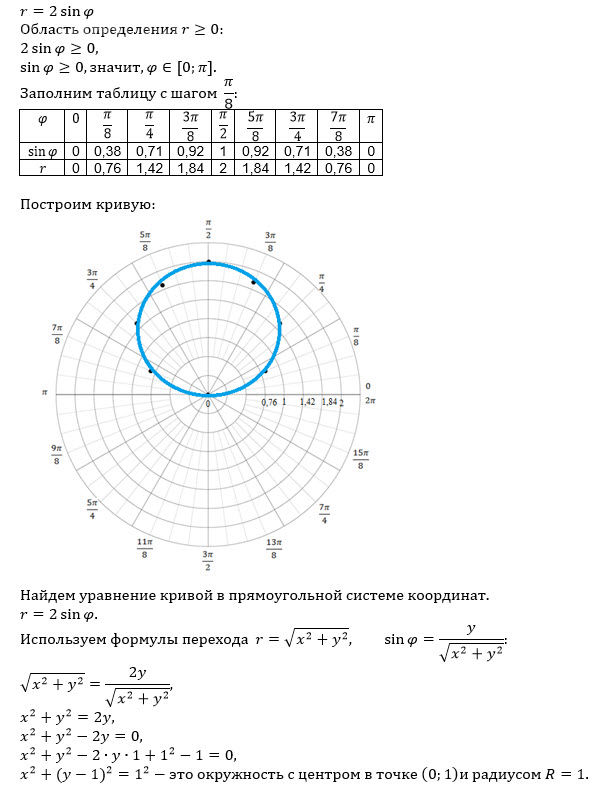
Все решения
r = 2 sin φ (1)
дано в полярных координатах (r, φ). Ниже – что обычно просят сделать с таким выражением и подробное объяснение каждого шага.
──────────────────────
1. КАКАЯ ЭТО ЛИНИЯ?
──────────────────────
Запишем связь между полярными и декартовыми координатами:
x = r cos φ, y = r sin φ, r = √(x² + y²).
Подставим r из (1) в r = √(x² + y²):
√(x² + y²) = 2 sin φ. (2)
Но sin φ = y / r = y / √(x² + y²).
Умножаем (2) на √(x² + y²):
x² + y² = 2y. (3)
Переносим 2y влево и группируем квадрат:
x² + y² − 2y = 0
x² + (y² − 2y +1) = 1
x² + (y − 1)² = 1. (4)
Уравнение (4) – окружность
• центр C (0, 1);
• радиус R = 1.
Следовательно, (1) описывает окружность радиуса 1, сдвинутую на 1 единицу вверх от начала координат.
──────────────────────
2. ДОПУСТИМЫЕ УГЛЫ Φ
──────────────────────
Для 0 ≤ φ ≤ π величина sin φ неотрицательна, поэтому r ≥ 0 и окружность обходится один раз целиком (φ = 0 и φ = π дают r = 0 – верхняя и нижняя точки).
При φ за пределами [0, π] синус отрицателен; тогда r становится отрицательным, что эквивалентно положительному радиусу под углом φ + π. Итоговый геометрический образ остаётся той же окружностью.
──────────────────────
3. ПЛОЩАДЬ (если требуется)
──────────────────────
Проверим, что площадь равна πR² = π:
A = ½ ∫₀^π r² dφ = ½ ∫₀^π (2 sin φ)² dφ
= 2 ∫₀^π sin² φ dφ = 2·π/2 = π.
──────────────────────
4. КЛЮЧЕВОЕ
──────────────────────
Уравнение r = 2 sin φ задаёт окружность
x² + (y − 1)² = 1.
Центр (0, 1), радиус 1; полный обход при 0 ≤ φ ≤ π.