Задача 80530 Нужно решить уравнение...
Условие
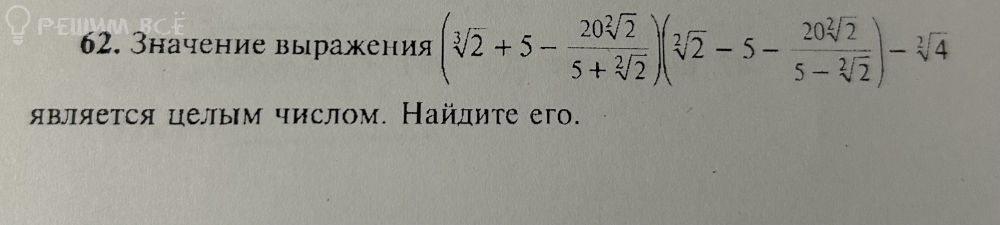
Решение
Тогда данное выражение имеет вид
( t + 5 − 20t/(5 + t) )·( t − 5 − 20t/(5 − t) ) − √4. (1)
1. Найдём первое скобочное выражение
A = t + 5 − 20t/(5 + t)
= [(t + 5)(5 + t) − 20t] /(5 + t)
= [(5 + t)² − 20t] /(5 + t).
(5 + t)² = 25 + 10t + t² = 25 + 10t + 2 = 27 + 10t,
следовательно
A = (27 + 10t − 20t)/(5 + t) = (27 − 10t)/(5 + t). (2)
2. Найдём второе скобочное выражение
B = t − 5 − 20t/(5 − t)
= [(t − 5)(5 − t) − 20t] /(5 − t).
(t − 5)(5 − t) = −(t − 5)² = −[(5 − t)²]
= −(25 − 10t + t²)
= −(25 − 10t + 2) = −(27 − 10t) = 10t − 27,
поэтому
B = (10t − 27 − 20t)/(5 − t) = (−10t − 27)/(5 − t). (3)
3. Перемножим (2) и (3):
A·B = (27 − 10t)(−10t − 27) / [(5 + t)(5 − t)]
= −(27 − 10t)(10t + 27) / (25 − t²).
Так как t² = 2, то знаменатель равен 25 − 2 = 23.
Числитель:
(27 − 10t)(10t + 27) = 27·10t + 27·27 − 100t² − 270t
= 270t + 729 − 200 − 270t
= 529.
С учётом минуса перед скобкой имеем числитель −529.
Значит
A·B = −529 / 23 = −23. (4)
4. Подставляем (4) в (1) и учитываем √4 = 2:
(1) = −23 − 2 = −25. (5)
Получили целое число −25. Ответ: −25.
Все решения
