Задача 80513 Доковое реоро правильной четырехугольной...
Условие
Решение
Хоть бы проверили на ошибки. Перевожу на русский язык:
[b]Боковое ребро правильной четырехугольной пирамиды
равно 13 см.
Найдите площадь полной поверхности пирамиды,
если её апофема равна 12 см.[/b]
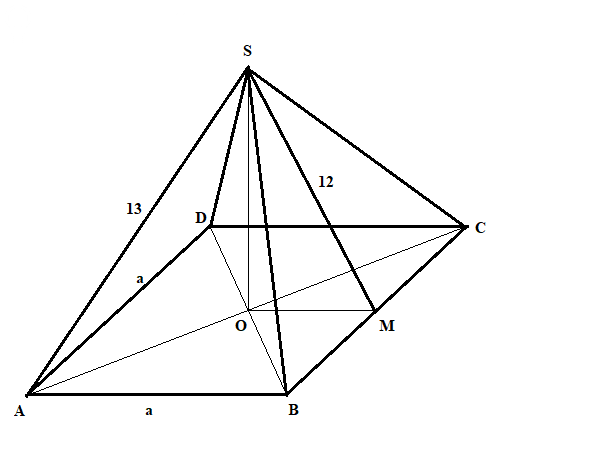
Смотрите рисунок.
Формализуем задачу.
Дано:
ABCDS - правильная 4-угольная пирамида
SA = 13 см - боковое ребро.
SM = 12 см - апофема, M - середина ребра BC.
Найти:
S(полн) = ?
Решение:
Так как пирамида правильная, то все боковые рёбра равны
и в основании лежит квадрат.
SA = SB = SC = SD = 13 см
AB = BC = CD = DA = a см
Обозначим О центр основания. Рассмотрим треугольник SBM.
Он прямоугольный, поэтому по теореме Пифагора:
BM = sqrt(SB^2 - SM^2) = sqrt(13^2 - 12^2) = sqrt(169 - 144) = sqrt(25) = 5 см
Но М - середина стороны BC, поэтому:
BC = a = 2*BM = 2*5 = 10 см.
Теперь можно найти площади основания и боковой поверхности:
S(осн) = a^2 = 10^2 = 100 см^2
S(SBC) = BC*SM/2 = 10*12/2 = 60 см^2
Боковая поверхность состоит из 4 одинаковых треугольников:
S(бок) = 4*S(SBC) = 4*60 = 240 см^2
Полная поверхность состоит из основания и боковой поверхности:
S(полн) = S(осн) + S(бок) = 100 + 240 = 340 см^2
Ответ: 340