Задача 80510 Помогите решить 4 и 5 задание ...
Условие
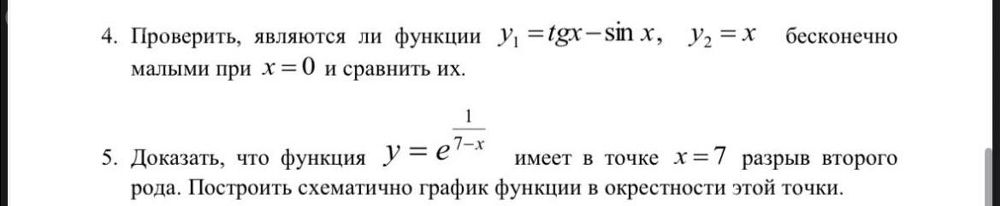
Решение
[m]lim_{x → 0}y_{1}(x)=[m]lim_{x → 0}(tgx-sinx)=0[/m]
Функция [m] y_{1}(x)[/m] бесконечно малая по определению
[m]lim_{x → 0}y_{2}(x)=[m]lim_{x → 0}x=0[/m]
Функция [m] y_{2}(x)[/m] бесконечно малая по определению
[m]lim_{x → 0}\frac{y_{1}(x)}{y_{2}(x)}=lim_{x → 0}\frac{tgx-sinx}{x}=lim_{x → 0}\frac{sinx\cdot (\frac{1}{cosx}-1)}{x}=lim_{x → 0}\frac{sinx}{x}\cdot lim_{x → 0}\frac{1-cosx}{cosx}=1\cdot 0=0 [/m]
[m]tgx-sinx=o(x)[/m] ( см. определение 7)
5.
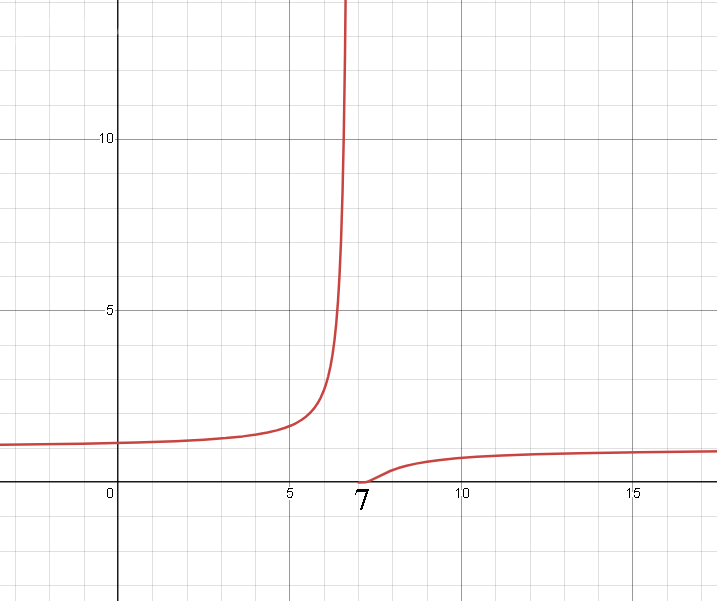
Функция не определена в точке x=7, так как (7-х) - знаменатель дроби (1/(7-х))
Находим предел функции в этой точке слева
lim_(x→7 -0) f(x)=e^(lim_(x→7 -0)1/(7-x))=7^(+∞)=+ ∞
Находим предел функции в этой точке слева
lim_(x→ 7+0) f(x)=e^(lim_(x→7 +0)1/(7-x))=e^(-∞)=0
Левосторонний предел равен ∞ ,
значит х=7 - точка разрыва второго рода.