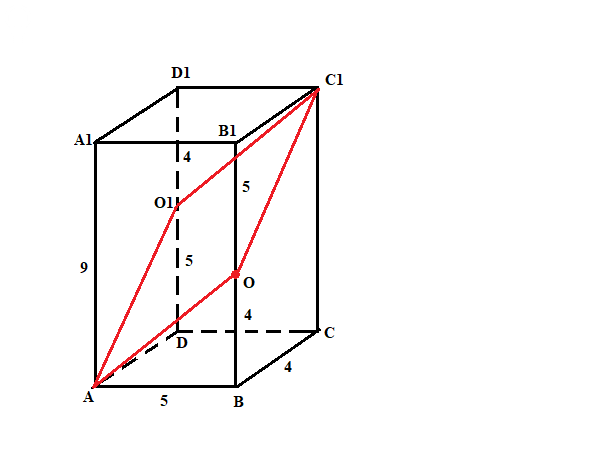
Задача 80503 В прямоугольном параллелепипеде...

69105f17525fe60eef339f92

11/9/2025 9:30:30 AM

В прямоугольном параллелепипеде ????????????????????1????1????1????1 известны рёбра ???????? = 5,
???????? = 4, ????????1 = 9. Точка O принадлежит ребру ????????1 и делит его в отношении
4:5, считая от вершины B. Найдите площадь сечения этого параллелепипеда
плоскостью, проходящей через точки ????, ???? и С1.

626fab9a354ab65fb2f43abb

11/9/2025 4:28:43 PM

★

Сечение показано на рисунке.
Это параллелограмм AOC1O1.
Так как сечение это плоскость, то на параллельных гранях параллелепипеда оно даст параллельные отрезки.
AO || C1O1, AO1 || C1O
Так как точка O делит ребро BB1 в отношении 4:5, а длина |BB1| = 9, то
|BO| = 4, |OB1| = 5, |DO1| = 5, |O1D1| = 4
Длины сторон параллелограмма AOC1O1 по теореме Пифагора:
|AO| = sqrt(|AB|^2 + |BO|^2) = sqrt(5^2 + 4^2) = sqrt(25 + 16) = sqrt(41)
|OC1| = sqrt(|C1B1|^2 + |B1O|^2) = sqrt(4^2 + 5^2) = sqrt(16 + 25) = sqrt(41)
Так как у параллелограмма стороны равны, то это ромб.
Найдем угол между его сторонами.
Большая диагональ AC1:
|AC1| = sqrt(|AB|^2 + |BC|^2 + |CC1|^2) = sqrt(5^2 + 4^2 + 9^2) = sqrt(122)
По теореме косинусов для треугольника AOC1:
|AC1|^2 = |AO|^2 + |OC1|^2 - 2*|AO|*|OC1|*cos AOC1
122 = 41 + 41 - 2*sqrt(41)*sqrt(41)*cos AOC1
122 = 82 - 2*41*cos AOC1 = 82*(1 - cos AOC1)
1 - cos AOC1 = 122/82 = 61/41
cos AOC1 = 1 - 61/41 = -20/41
cos^2 AOC1 = 400/1681
sin^2 AOC1 = 1 - cos^2 AOC1 = 1 - 400/1681 = 1281/1681
sin AOC1 = sqrt(1281)/41
Площадь ромба:
S = |AO|*|OC1|*sin AOC1
S = sqrt(41)*sqrt(41)*sqrt(1281)/41 = sqrt(1281) ≈ 35,8