Задача 80491 Высота девятиэтажного дома составляет 30...
Условие
Решение
И у него всё правильно.
А я напишу для случая, когда башня выше дома.
Смотрите рисунок.
Расстояние от дома до башни обозначим L, высоту башни H.
Разность в высоте башни и дома равна H - 30.
Тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему катету.
{ tg 18° = (H - 30)/L
{ tg 27° = H/L
Выразим L во 2 уравнении:
L = H/tg 27°
Подставим его в первое уравнение:
tg 18° = (H - 30) : (H/tg 27°)
tg 18° = tg 27°*(H - 30)/H
H*tg 18° = H*tg 27° - 30*tg 27°
30*tg 27° = H*(tg 27° - tg 18°)
H = 30*tg 27° / (tg 27° - tg 18°)
С точностью до тысячных:
tg 27° ≈ 0,510; tg 18° ≈ 0,325
Высота башни:
H = 30*0,510 / (0,510 - 0,325) = 30*0,510/0,185 ≈ 82,703 м
С точностью до сотых долей метра:
H = 82,70 м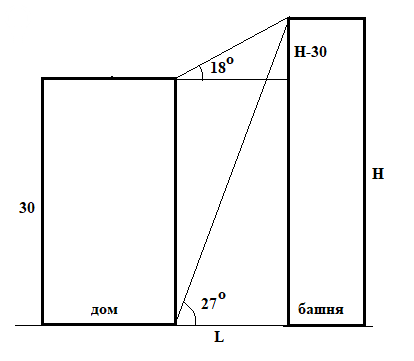
Все решения
В – основание девятиэтажного дома,
А – его крыша (АВ = 30 м),
Т – вершина башни,
х – горизонтальное расстояние между зданиями,
h – искомая высота башни.
1. Из нижней точки В вершина башни видна под углом подъёма 27°:
tg 27° = h / х ⇒ х = h / tg 27°. (1)
2. Из верхней точки А вершина башни наблюдается под углом снижения 18°;
вертикальный перепад АТ равен 30 − h, поэтому
tg 18° = (30 − h) / х. (2)
3. Подставим выражение (1) в (2):
tg 18° = (30 − h) / (h / tg 27°)
tg 18° = (30 − h)·tg 27° / h
⇒ h (tg 18° + tg 27°) = 30·tg 27°
⇒ h = 30·tg 27° / (tg 18° + tg 27°).
4. Подсчитаем (значения тригонометрических функций округлены до тысячных):
tg 18° ≈ 0,325,
tg 27° ≈ 0,510.
Тогда
h ≈ 30·0,510 / (0,325 + 0,510)
≈ 15,300 / 0,835
≈ 18,318 м.
5. Окончательно (до сотых долей метра):
h ≈ 18,32 м.
Ответ: высота башни равна примерно 18,32 м.