Задача 80487 Решить систему уравнений методом Гауса...
Условие
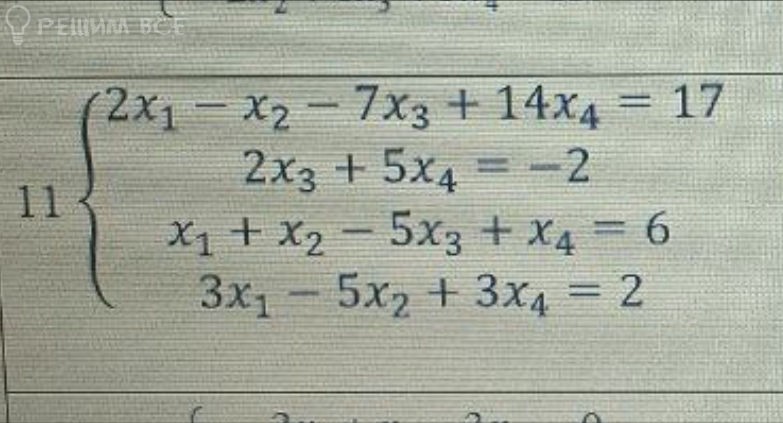
Решение
{ 2x3 + 5x4 = -2
{ x1 + x2 - 5x3 + x4 = 6
{ 3x1 - 5x2 + 3x4 = 2
Перепишем систему с 0 коэффициентами:
{ 2x1 - x2 - 7x3 + 14x4 = 17
{ 0x1 + 0x2 + 2x3 + 5x4 = -2
{ x1 + x2 - 5x3 + x4 = 6
{ 3x1 - 5x2 + 0x3 + 3x4 = 2
Переходим к расширенной матрице:
[m]\begin{pmatrix}
2 & -1 & -7 & 14 & | & 17 \\
0 & 0 & 2 & 5 & | & -2 \\
1 & 1 & -5 & 1 & | & 6 \\
3 & -5 & 0 & 3 & | & 2 \\
\end{pmatrix}[/m]
Меняем местами строки, от этого систему не меняется:
[m]\begin{pmatrix}
1 & 1 & -5 & 1 & | & 6 \\
2 & -1 & -7 & 14 & | & 17 \\
0 & 0 & 2 & 5 & | & -2 \\
3 & -5 & 0 & 3 & | & 2 \\
\end{pmatrix}[/m]
Умножаем 1 строку на -2 и складываем со 2 строкой.
Умножаем 1 строку на -3 и складываем со 4 строкой.
[m]\begin{pmatrix}
1 & 1 & -5 & 1 & | & 6 \\
0 & -3 & 3 & 12 & | & 5 \\
0 & 0 & 2 & 5 & | & -2 \\
0 & -8 & 15 & 0 & | & -16 \\
\end{pmatrix}[/m]
Умножаем 2 строку на 8, а 4 строку на -3. Сумму пишем в 4 строку.
[m]\begin{pmatrix}
1 & 1 & -5 & 1 & | & 6 \\
0 & -3 & 3 & 12 & | & 5 \\
0 & 0 & 2 & 5 & | & -2 \\
0 & 0 & -21 & 96 & | & 88 \\
\end{pmatrix}[/m]
Умножаем 3 строку на 21, а 4 строку на 2. Сумму пишем в 4 строку.
[m]\begin{pmatrix}
1 & 1 & -5 & 1 & | & 6 \\
0 & -3 & 3 & 12 & | & 5 \\
0 & 0 & 2 & 5 & | & -2 \\
0 & 0 & 0 & 297 & | & 134 \\
\end{pmatrix}[/m]
Возвращаемся к системе:
{ x1 + x2 - 5x3 + x4 = 6
{ 0x1 - 3x2 + 3x3 + 12x4 = 5
{ 0x1 + 0x2 + 2x3 + 5x4 = -2
{ 0x1 + 0x2 +0x3 + 297x4 = 134
Из 4 уравнения:
[b]x4 = 134/297[/b]
Подставляем в 3 уравнение:
2x3 + 5*134/297 = -2
2x3 = -594/297 - 670/297 = -1264/297
[b]x3 = -632/297[/b]
Подставляем во 2 уравнение:
-3x2 + 3(-632/297) + 12*134/297 = 5
-3x2 = 1485/297 + 1896/297 - 1608/297 = 1773/297
[b]x2 = -591/297 = -197/99[/b]
Подставляем в 1 уравнение:
x1 - 591/297 - 5*(-632/297) + 134/297 = 6
x1 = 1782/297 + 591/297 - 3160/297 - 134/297 = -921/297
[b]x1 = -921/297 = -307/99[/b]
[b]Ответ: x1 = -307/99; x2 = -197/99; x3 = -632/297; x4 = 134/297[/b]