Задача 80485 Исследовать функцию и построить её...
Условие
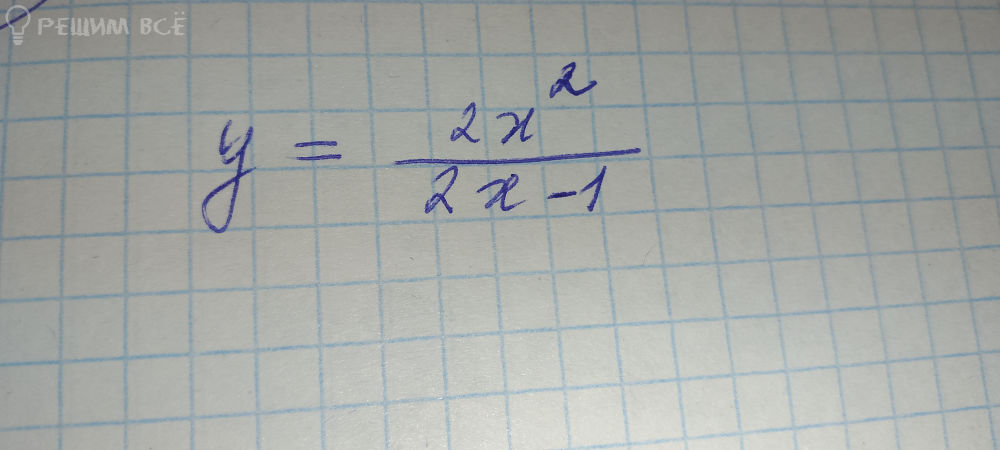
Решение
План исследования функции.
1. Найти область определения. Выделить особые точки (точки разрыва).
2x - 1 ≠ 0
x ≠ 1/2 - неустранимый разрыв II вида.
[b]x ∈ (-oo; 1/2) U (1/2; +oo)[/b]
2. Проверить наличие вертикальных асимптот в точках разрыва и на границах области определения.
[b]Вертикальная асимптота в точке x = 1/2.[/b]
3. Найти точки пересечения с осями координат и промежутки знакопостоянства.
[b]y(0) = 0[/b]
Пересечение с осями в начале координат.
4. Определить, является ли функция чётной или нечётной.
[m]\large y(-x) = \frac{2(-x)^2}{2(-x)-1} = \frac{2x^2}{-2x-1}[/m]
y(-x) ≠ -y(x); y(-x) ≠ y(x)
[b]Функция не чётная и не нечётная.[/b]
5. Определить, является ли функция периодической (для тригонометрических функций).
[b]Функция не периодическая.[/b]
6. Найти точки экстремума и интервалы возрастания-убывания.
Точки экстремума - это точки, в которых y'(x) = 0
[m]\large y'(x) =(\frac{2x^2}{2x-1})' = \frac{4x(2x - 1) - 2x^2 \cdot 2}{(2x - 1)^2} =[/m]
[m]\large = \frac{8x^2 - 4x - 4x^2}{(2x - 1)^2} = \frac{4x^2 - 4x}{(2x - 1)^2}[/m]
[m]\large \frac{4x^2 - 4x}{(2x - 1)^2} = 0[/m]
Если дробь равна 0, то числитель равен 0, а знаменатель нет.
4x^2 - 4x = 0
x^2 - x = 0
x(x - 1) = 0
x1 = 0; x2 = 1
Интервалы.
При x < 0 будет y'(x) > 0 - функция возрастает
При x ∈ (0; 1/2) будет y'(x) < 0 - функция убывает.
[b]x = 0 - точка максимума.[/b]
При x ∈ (1/2; 1) будет y'(x) < 0 - функция убывает.
При x > 1 будет y'(x) > 0 - функция возрастает
[b]x = 1 - точка минимума.[/b]
7. Найти точки перегиба и интервалы выпуклости-вогнутости.
Точки перегиба - это точки, где y''(x) = 0
[m]\large y''(x) = (\frac{4x^2 - 4x}{(2x - 1)^2})' = \frac{(8x - 4)(2x - 1)^2 - (4x^2 - 4x) \cdot 2(2x - 1) \cdot 2}{(2x - 1)^4}= [/m]
[m]\large = \frac{(8x - 4)(2x - 1) - (4x^2 - 4x) \cdot 4}{(2x - 1)^3} = \frac{16x^2 - 8x - 8x + 4 - 16x^2 + 16x}{(2x - 1)^3} =[/m]
[m]=\frac{4}{(2x - 1)^3} = 0[/m]
Это уравнение корней не имеет.
[b]Точек перегиба нет.[/b]
8. Найти наклонные асимптоты. Исследовать поведение на бесконечности.
Наклонные асимптоты имеют вид:
f(x) = kx + b, где:
[m]\large k = \lim \limits_{x \to \infty} \frac{y(x)}{x} = \lim \limits_{x \to \infty} \frac{2x}{2x - 1} = 1[/m]
[m]\large b = \lim \limits_{x \to \infty} (y(x) - kx) = \lim \limits_{x \to \infty} (\frac{2x^2}{2x - 1} - x) = [/m]
[m]\large = \lim \limits_{x \to \infty} \frac{2x^2 - 2x^2 + x}{2x - 1}= \lim \limits_{x \to \infty} \frac{x}{2x - 1} = \frac{1}{2}[/m]
[b]f(x) = x + 1/2[/b]
9. Выбрать дополнительные точки и вычислить их координаты (при необходимости).
x = 0; y(0) = 0
x = 1; y(1) = 2/(2*1 - 1) = 2/1 = 2
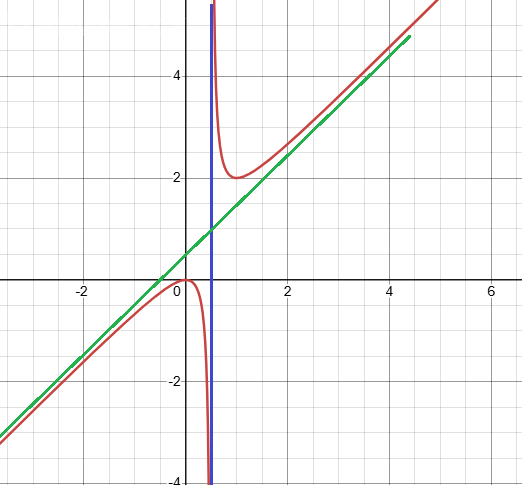
10. Построить график функции, ее асимптот, отметить ключевые точки.
График на рисунке.
Вертикальная асимптота показана синим, наклонная - зелёным.