Задача 8048 Отрезки AB и CD являются хордами...

slava191

23.03.2016

Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 20 , CD = 48, а расстояние от центра окружности до хорды AB равно 24.

Расстояние от точки до прямой - это перпендикуляр, опущенный к этой прямой, а перпендикуляр, опущенный из центра окружности к хорде, делит ее пополам (свойство). Значит АО1=ВО1=20/2=10 и СО2=DО2=48/2=24.

По теореме Пифагора BO= sqrt(BO1^(2)+ OO1^(2))= sqrt(10^(2)+ 24^(2))= 26.

ВО и ОД - это радиусы, а значит они равны. По теореме того же Пифагора OO2= sqrt(OD^(2)- DO2^(2)) = sqrt(26^(2)- 24^(2)) = 10.

Значит, искомое расстояние равно 10.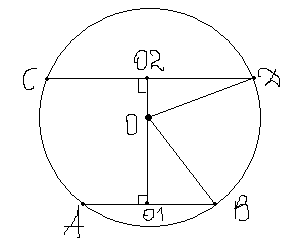

Ответ: 10