Задача 80477 На одном фото представлено условие...
Условие
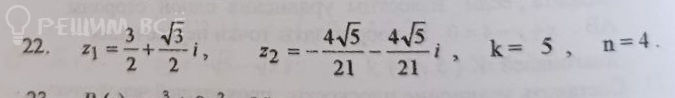

Решение
[m]z2=\frac{4 \sqrt{5}}{21}-\frac{4 \sqrt{5}}{21} \cdot i[/m]
а) Найти в алгебраической форме:
[m]z1 + z2 = \frac{3}{2}+\frac{\sqrt{3}}{2} \cdot i + \frac{4 \sqrt{5}}{21}-\frac{4 \sqrt{5}}{21} \cdot i = \frac{63 + 8\sqrt{5}}{42} + \frac{21\sqrt{3} - 8\sqrt{5}}{42} \cdot i[/m]
[m]z1 - z2 = \frac{3}{2}+\frac{\sqrt{3}}{2} \cdot i - \frac{4 \sqrt{5}}{21}+\frac{4 \sqrt{5}}{21} \cdot i = \frac{63 - 8\sqrt{5}}{42} + \frac{21\sqrt{3} + 8\sqrt{5}}{42} \cdot i[/m]
[m]z1 \cdot z2 = ( \frac{3}{2}+\frac{\sqrt{3}}{2} \cdot i ) \cdot (\frac{4 \sqrt{5}}{21}-\frac{4 \sqrt{5}}{21} \cdot i ) =[/m]
[m]= \frac{12\sqrt{5}}{42} + \frac{4 \sqrt{15}}{42} \cdot i - \frac{12\sqrt{5}}{42} \cdot i + \frac{4 \sqrt{15}}{42} =[/m]
[m]= \frac{12\sqrt{5} + 4 \sqrt{15}}{42} + \frac{4 \sqrt{15} - 12\sqrt{5}}{42} \cdot i = \frac{2 \sqrt{15}}{21} \cdot (\sqrt{3} + 1 - (\sqrt{3} - 1) \cdot i)[/m]
[m]\large \frac{z1}{z2} = \frac{ \frac{3}{2}+\frac{\sqrt{3}}{2} \cdot i}{\frac{4 \sqrt{5}}{21}-\frac{4 \sqrt{5}}{21} \cdot i } =\frac{(\frac{3}{2}+\frac{\sqrt{3}}{2} \cdot i)(\frac{4 \sqrt{5}}{21}+\frac{4 \sqrt{5}}{21} \cdot i)}{(\frac{4 \sqrt{5}}{21}-\frac{4 \sqrt{5}}{21} \cdot i)(\frac{4 \sqrt{5}}{21}+\frac{4 \sqrt{5}}{21} \cdot i)} =[/m]
[m]\large = \frac{(\frac{12\sqrt{5}}{42}+\frac{4 \sqrt{15}}{42} \cdot i + \frac{12\sqrt{5}}{42} \cdot i - \frac{4 \sqrt{15}}{42}}{\frac{16 \cdot 5}{441} + \frac{16 \cdot 5}{441}} =\frac{\frac{12\sqrt{5}-4 \sqrt{15}}{42}+\frac{12\sqrt{5}+4 \sqrt{15}}{42} \cdot i}{\frac{160}{441}} =[/m]
[m]\large = \frac{12\sqrt{5}-4 \sqrt{15} + (12\sqrt{5}+4 \sqrt{15}) \cdot i}{42} \cdot \frac{441}{160}= \frac{21(3\sqrt{5} - \sqrt{15}) + (3\sqrt{5} + \sqrt{15}) \cdot i}{80} =[/m]
[m]\large = \frac{21\sqrt{15}}{80} \cdot (\sqrt{3} - 1 + (\sqrt{3} + 1) \cdot i)[/m]
б) Найти в тригонометрической форме при k = 5; n = 4
[m]|z1| = \sqrt{(\frac{3}{2})^2 + (\frac{\sqrt{3}}{2})^2} = \sqrt{\frac{9}{4} + \frac{3}{4}} = \sqrt{\frac{12}{4}} = \sqrt{3}[/m]
[m]z1 = \sqrt{3} \cdot (\frac{\sqrt{3}}{2} + \frac{1}{2} \cdot i) = \sqrt{3} \cdot (\cos \frac{\pi}{6} + i \cdot \sin \frac{\pi}{6})[/m]
[m]|z2| = \sqrt{(\frac{4 \sqrt{5}}{21})^2 + (-\frac{4 \sqrt{5}}{21})^2} = \sqrt{\frac{16 \cdot 5}{441} + \frac{16 \cdot 5}{441}} = \sqrt{\frac{160}{441}} = \frac{4 \sqrt{10}}{21}[/m]
[m]z2 = \frac{4 \sqrt{10}}{21} \cdot (\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{2}} \cdot i) = \frac{4 \sqrt{10}}{21} \cdot (\cos \frac{7\pi}{4} + i \cdot \sin \frac{7\pi}{4})[/m]
[m]z1 \cdot z2 = \sqrt{3} \cdot (\cos \frac{\pi}{6} + i \cdot \sin \frac{\pi}{6}) \cdot \frac{4 \sqrt{10}}{21} \cdot (\cos \frac{7\pi}{4} + i \cdot \sin \frac{7\pi}{4}) =[/m]
[m]\frac{4 \sqrt{30}}{21}(\cos \frac{\pi}{6} \cos \frac{7\pi}{4} + i \cdot \sin \frac{\pi}{6} \cos \frac{7\pi}{4} + i \cdot \cos \frac{\pi}{6} \sin \frac{7\pi}{4} - \sin \frac{\pi}{6} \sin \frac{7\pi}{4}) =[/m]
[m]=\frac{4 \sqrt{30}}{21}(\cos (\frac{\pi}{6} + \frac{7\pi}{4}) + i \cdot \sin (\frac{\pi}{6} + \frac{7\pi}{4})) = [/m]
[m]= \frac{4 \sqrt{30}}{21} (\cos \frac{23\pi}{12} + i \cdot \sin \frac{23\pi}{12}) = [/m]
[m]= \frac{4 \sqrt{30}}{21} (\cos (-\frac{\pi}{12}) - i \cdot \sin \frac{\pi}{12})[/m]
[m]\large \frac{z1}{z2} = \frac{\sqrt{3} \cdot (\cos \frac{\pi}{6} + i \cdot \sin \frac{\pi}{6})}{\frac{4 \sqrt{10}}{21} \cdot (\cos \frac{7\pi}{4} + i \cdot \sin \frac{7\pi}{4})} =[/m]
[m]\large = \frac{21\sqrt{3}}{4 \sqrt{10}} \cdot \frac{(\cos \frac{\pi}{6} + i \cdot \sin \frac{\pi}{6})(\cos \frac{7\pi}{4} - i \cdot \sin \frac{7\pi}{4})}{(\cos \frac{7\pi}{4} + i \cdot \sin \frac{7\pi}{4})(\cos \frac{7\pi}{4} - i \cdot \sin \frac{7\pi}{4})} =[/m]
[m]\large = \frac{21\sqrt{30}}{4 \cdot 10} \cdot \frac{\cos \frac{\pi}{6} \cos \frac{7\pi}{4} + i \cdot \sin \frac{\pi}{6} \cos \frac{7\pi}{4} - i \cdot \cos \frac{\pi}{6} \sin \frac{7\pi}{4} + \sin \frac{\pi}{6} \sin \frac{7\pi}{4}}{\cos^2 \frac{7\pi}{4} + \sin^2 \frac{7\pi}{4}} =[/m]
[m]\large = \frac{21\sqrt{30}}{40} \cdot \frac{(\cos \frac{\pi}{6} \cos \frac{7\pi}{4} +\sin \frac{\pi}{6} \sin \frac{7\pi}{4}) + i \cdot (\sin \frac{\pi}{6} \cos \frac{7\pi}{4} - \cos \frac{\pi}{6} \sin \frac{7\pi}{4})}{1} = [/m]
[m]\large = \frac{21\sqrt{30}}{40} \cdot (\cos(\frac{7\pi}{4} - \frac{\pi}{6}) + i \cdot \sin(\frac{\pi}{6} - \frac{7\pi}{4})) =[/m]
[m]\large = \frac{21\sqrt{30}}{40} \cdot (\cos \frac{19\pi}{12} - \sin \frac{19\pi}{12})[/m]
[m]z1^{k} = (\sqrt{3} \cdot (\cos \frac{\pi}{6} + i \cdot \sin \frac{\pi}{6}))^5 = (\sqrt{3})^5 \cdot (\cos \frac{5\pi}{6} + i \cdot \sin \frac{5\pi}{6}) =[/m]
[m]= \sqrt{243} \cdot (\cos \frac{5\pi}{6} + i \cdot \sin \frac{5\pi}{6})[/m]
[m]\sqrt[n]{z2} = \sqrt[4]{\frac{4 \sqrt{10}}{21} \cdot (\cos \frac{7\pi}{4} + i \cdot \sin \frac{7\pi}{4})}[/m]
Корень принимает 4 значения: x0, x1, x2, x3
[m]x0 = \sqrt[4]{\frac{4 \sqrt{10}}{21}} \cdot (\cos \frac{\frac{7\pi}{4} + 2π \cdot 0}{4} + i \cdot \sin \frac{\frac{7\pi}{4} + 2π \cdot 0}{4}) =[/m]
[m]= \sqrt[4]{\frac{4 \sqrt{10}}{21}} \cdot (\cos \frac{7\pi}{16} + i \cdot \sin \frac{7\pi}{16})[/m]
[m]x1 = \sqrt[4]{\frac{4 \sqrt{10}}{21}} \cdot (\cos \frac{\frac{7\pi}{4} + 2π \cdot 1}{4} + i \cdot \sin \frac{\frac{7\pi}{4} + 2π \cdot 1}{4}) = [/m]
[m]= \sqrt[4]{\frac{4 \sqrt{10}}{21}} \cdot (\cos \frac{15\pi}{16} + i \cdot \sin \frac{15\pi}{16})[/m]
[m]x2 = \sqrt[4]{\frac{4 \sqrt{10}}{21}} \cdot (\cos \frac{\frac{7\pi}{4} + 2π \cdot 2}{4} + i \cdot \sin \frac{\frac{7\pi}{4} + 2π \cdot 2}{4}) = [/m]
[m]= \sqrt[4]{\frac{4 \sqrt{10}}{21}} \cdot (\cos \frac{23\pi}{16} + i \cdot \sin \frac{23\pi}{16})[/m]
[m]x3 = \sqrt[4]{\frac{4 \sqrt{10}}{21}} \cdot (\cos \frac{\frac{7\pi}{4} + 2π \cdot 3}{4} + i \cdot \sin \frac{\frac{7\pi}{4} + 2π \cdot 3}{4}) = [/m]
[m]= \sqrt[4]{\frac{4 \sqrt{10}}{21}} \cdot (\cos \frac{31\pi}{16} + i \cdot \sin \frac{31\pi}{16})[/m]