Задача 80475 ...
Условие
Решение
y= ρ sin θ
x^2+y^2= ρ ^2cos^2 θ + ρ ^2sin^2 θ= ρ ^2*(cos^2 θ +sin^2 θ )= ρ ^2*1= ρ ^2
Уравнение принимает вид:
(ρ ^2)^3=18*ρ cos θ *ρ sin θ
так как
2cos θ * sin θ = sin 2θ
то
ρ ^6=9*ρ^2 sin 2 θ ⇒
ρ ^4=9sin2 θ
[m] ρ =\sqrt[4]{9sin 2θ} [/m]
sin 2θ ≥ 0 ⇔ θ ∈ [0 ° , 90 °] υ [180 ° ,270 °]
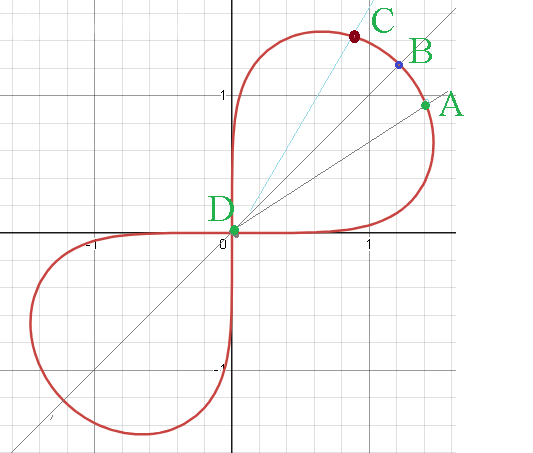
График в 1 и 3 четвертях
θ =30 ° ⇒ [m] ρ =\sqrt[4]{9sin 60°} [/m]
Получаем точку
А (30 ° ; [m] \sqrt[4]{\frac{9\sqrt{3}}{2}} [/m])
θ =45 ° ⇒ [m] ρ =\sqrt[4]{9sin 90°} [/m]
Получаем точку
В (45 ° ; [m] \sqrt[4]{9} [/m] )
θ =60 ° ⇒ [m] ρ =\sqrt[4]{9sin 120°} [/m]
получаем точку
С(60 ° ; [m] \sqrt[4]{\frac{9\sqrt{3}}{2}} [/m] )
θ =90 ° ⇒ ρ =[m] ρ =\sqrt[4]{9sin 180°} [/m]
sin180 ° =0
Получаем точку D
D(90 ° ; 0)