Задача 80474 Добрый день! Прошу решить уравнение по...
Условие



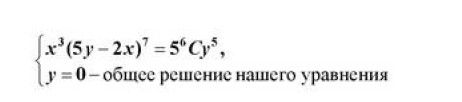
Решение
[m]x(2x-3y)dy=(-2y-1x)ydx[/m] - однородное уравнение
Замена:
[m]y=tx[/m]
Находим
[m]dy=tdx+xdt[/m]
Подставляем в исходное уравнение :
[m](2x^2-3x\cdot tx)(tdx+xdt)=(-2t^2x^2-x\cdot tx)dx[/m]
Раскрываем скобки
[m]2x^2tdx-3x^2t^2dx+2x^3dt-3tx^3dt=-2x^2t^2dx-tx^2dx[/m]
Собираем слагаем с dx слева, слагаемые с dt права
[m]2x^2tdx-3t^2x^2dx+2x^2t^2x^2dx+tx^2dx=3tx^3dt-2x^3dt[/m]
[m] (3x^2t - x^2t^2)dx=(3tx^3-2x^3)dt[/m] получили уравнение с разделяющимися переменными
[m] x^2t(3 - t)dx=(3t-2)x^3dt[/m]
[m]t(3 - t)dx=(3t-2)xdt[/m]
Разделяем переменные
[m]\frac{dx}{x}=\frac{(3t-2)dt}{t(3-t)}[/m] ( можем потерять решения: t=0; t=3; x=0)
Интегрируем
[m] ∫ \frac{dx}{x}= ∫ \frac{(3t-2)dt}{t(3-t)}[/m]
Чтобы проинтегрировать дробь раскладываем ее на простейшие методом неопределенных коэффициентов:
[m] \frac{(3t-2)}{t(3-t)}=\frac{A}{t}+\frac{B}{3-t}[/m]
[m]3t-2=A\cdot (3-t)+Bt[/m]
[m]3t-2=(B-A)t+3A[/m]
B-A=3
-2=3A
A=-2/3
B=7/3
[m] \frac{(3t-2)}{t(3-t)}=-\frac{\frac{2}{3}}{t}+\frac{\frac{7}{3}}{3-t}[/m]
[m] \frac{(3t-2)}{t(3-t)}=-\frac{\frac{2}{3}}{t}-\frac{\frac{7}{3}}{t-3}[/m]
Итак,
[m]∫ \frac{dx}{x}= ∫(-\frac{\frac{2}{3}}{t}-\frac{\frac{7}{3}}{t-3}) dt[/m]
[m]ln|x|=-\frac{2}{3}ln|t|-\frac{7}{3}ln|t-3|+lnC_{1}[/m] умножаем на 3
[m]3ln|x|=-2ln|t|-7ln|t-3|+lnC_{1}[/m]
Применяем свойства логарифмов:
[m]ln|x|^{3}=lnC\cdot |t|^{-2}\cdot |(t-3)|^{-7}[/m] где [m] C=3C_{1}[/m]
[m]t=\frac{y}{x}[/m]
[m]t^{-1}=\frac{x}{y}[/m]
[m]x^3=C\cdot (\frac{x}{y})^2\cdot (\frac{y}{x}-3)^{-7}[/m]
[m] y^2(y-3x)^7=C\cdot x^6[/m] - О Т В Е Т