Задача 80466 Можете решить, пожалуйста, только первые...
Условие


Решение
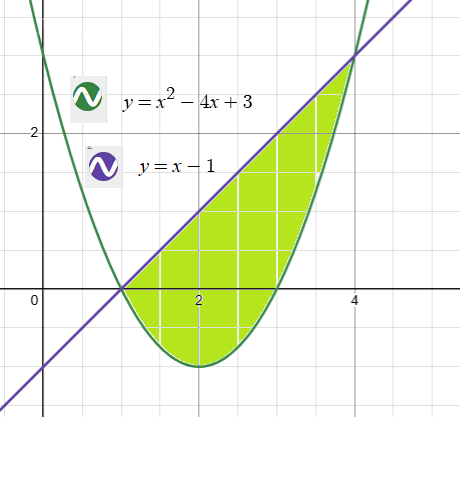
Чтобы найти ее площадь, сначала найдем границы интервала.
Для этого приравняем функции и найдем точки пересечения:
x^2 - 4x + 3 = x - 1
x^2 - 5x + 4 = 0
(x - 1)(x - 4) = 0
x1 = 1; x2 = 4
Чтобы найти площадь, берем интеграл от разности функций
[m]S = \int \limits_1^4 (x-1-x^2+4x-3)dx = \int \limits_1^4 (-x^2+5x-4)dx =[/m]
[m]= -\frac{x^3}{3} + \frac{5x^2}{2} - 4x \bigg |_1^4 =-\frac{4^3}{3} + \frac{5 \cdot 4^2}{2} - 4 \cdot 4 - (-\frac{1^3}{3} + \frac{5 \cdot 1^2}{2} - 4 \cdot 1) =[/m]
[m]= -\frac{64}{3} + 40 - 16 +\frac{1}{3} - \frac{5}{2} + 4 = [/m]
[m]= 28-\frac{63}{3}-\frac{5}{2} = 28 - 21 - 2,5 = 4,5[/m]
Ответ: S = 4,5
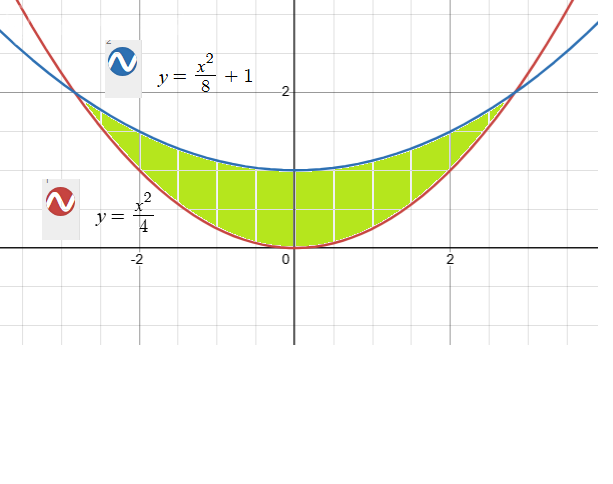
2) Смотрите рисунок 2.
Сначала найдем границы интервала.
Для этого приравняем функции и найдем точки пересечения:
[m]\frac{x^2}{4} = \frac{x^2}{8}+1[/m]
[m]\frac{2x^2}{8} - \frac{x^2}{8} = 1[/m]
[m]\frac{x^2}{8} = 1[/m]
x^2 = 8
x1 = - sqrt(8); x2 = sqrt(8)
Заметим, что фигура симметричная. Она состоит из двух одинаковых половин, одна при x < 0, вторая при x > 0.
Объем тела вращения фигуры вокруг оси Ox можно найти так:
[m]V=\pi \cdot \int \limits_{a}^{b} f^2(x) dx[/m]
В нашем случае объем равен двум интегралам от 0 до sqrt(8).
А функция f(x) - это разность функций двух парабол:
[m]f(x) = (\frac{x^2}{8}+1) - \frac{x^2}{4} = 1-\frac{x^2}{8}[/m]
Подставляем:
[m]V = 2\pi \cdot \int \limits_{0}^{\sqrt{8}} (1-\frac{x^2}{8})^2 dx = 2\pi \cdot \int \limits_{0}^{\sqrt{8}} (1-\frac{x^2}{4} + \frac{x^4}{64}) dx =[/m]
[m]= 2 \pi \cdot (x - \frac{x^3}{4 \cdot 3} + \frac{x^5}{64 \cdot 5}) \bigg |_{0}^{\sqrt{8}} = 2 \pi \cdot (\sqrt{8} - \frac{\sqrt{8}^3}{12} + \frac{\sqrt{8}^5}{64 \cdot 5}) = [/m]
[m]= 2 \pi \cdot (\sqrt{8} - \frac{8\sqrt{8}}{12} + \frac{64\sqrt{8}}{64 \cdot 5}) = 2 \pi \cdot (\sqrt{8} - \frac{\sqrt{8}}{3} + \frac{\sqrt{8}}{5}) =[/m]
[m]= 2 \pi \cdot (\frac{15\sqrt{8}}{15} - \frac{5\sqrt{8}}{15} + \frac{3\sqrt{8}}{15}) = 2 \pi \cdot \frac{13\sqrt{8}}{15} = \frac{26 \pi \sqrt{8}}{15}[/m]
Ответ: [m]V = \frac{26 \pi \sqrt{8}}{15}[/m]