Задача 80462 Математика. Подготовка к ЕГЭ-2026....
Условие
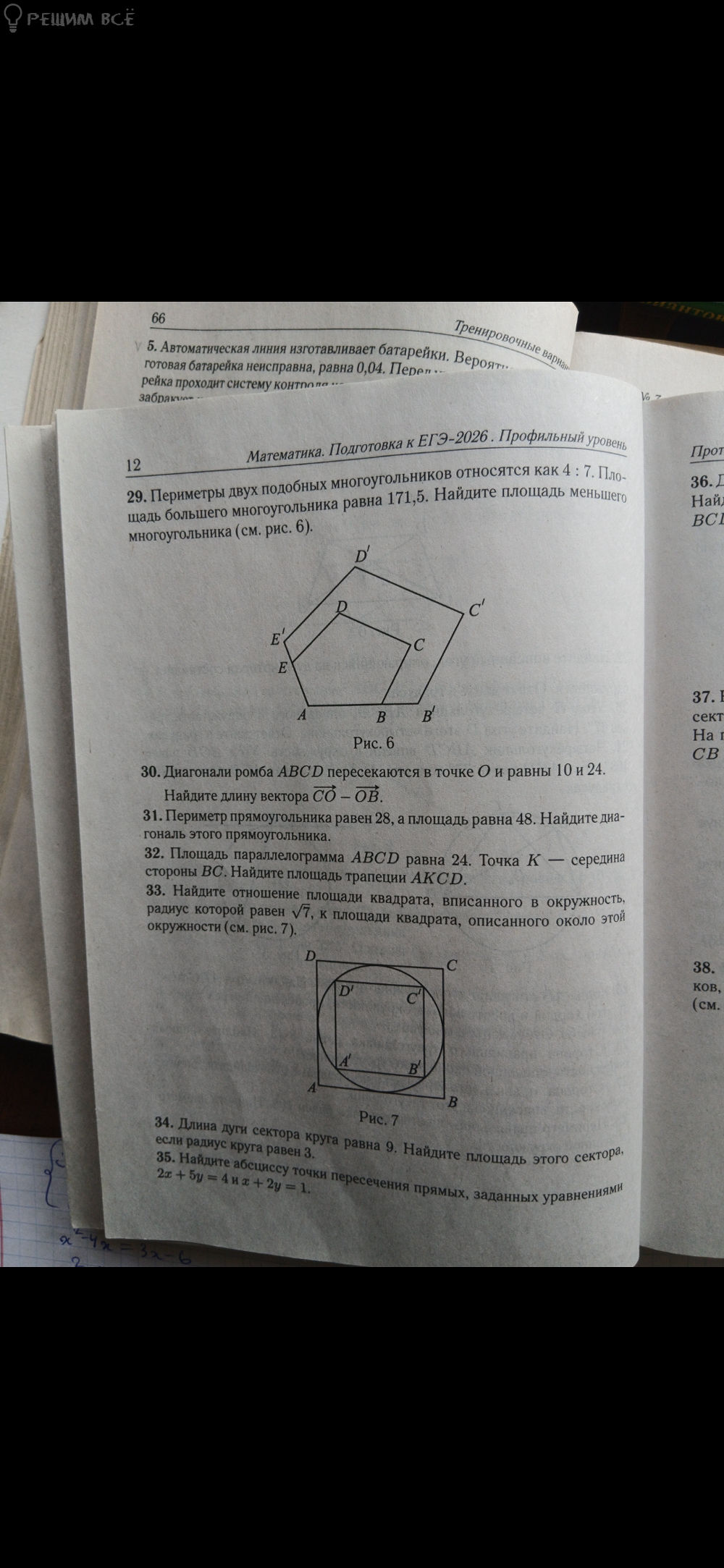
29. Периметры двух подобных многоугольников относятся как 4 : 7. Площадь большого многоугольника равна 171,5. Найдите площадь меньшего многоугольника (см. рис. 6).
30. Диагонали ромба ABCD пересекаются в точке O и равны 10 и 24. Найдите длину вектора [m]\overrightarrow{CO} - \overrightarrow{OB}[/m].
31. Периметр прямоугольника равен 28, а площадь равна 48. Найдите диагональ этого прямоугольника.
32. Площадь параллелограмма ABCD равна 24. Точка K — середина стороны BC. Найдите площадь трапеции AKCD.
33. Найдите отношение площадей квадрата, вписанного в окружность, радиус которой равен [m]\sqrt{7}[/m], к площади квадрата, описанного около этой окружности (см. рис. 7).
34. Длина дуги сектора круга равна 9. Найдите площадь этого сектора, если радиус круга равен 3.
35. Найдите абсциссу точки пересечения прямых, заданных уравнениями [m]2x + 5y = 4[/m] и [m]x + 2y = 1[/m].
Решение
Подобие многоугольников
P:P`=4:7=k ( коэффициент подобия)
S:S`=k^2=(4/7)^2
S`=171,5
S=[b](4/7)^2*171,5=56[/b]
30.
Диагонали взаимно перпендикулярны и в точке пересечения делятся пополам
значит из прямоугольного треугольника по теореме Пифагора
сторона ромба
a= √(5² + 12²) = √169 = 13.
vector{CO}-vector{OB}=vector{BC}
|vector{CO}-vector{OB}|=|vector{BC}|=a=13
Ответ: 13.
31. Прямоугольник:
P = 28,
S = 48
Система уравнений:
a + b = 14,
ab = 48.
Возводим первое уравнение в квадрат:
(a + b)² = a² + 2ab + b² ⇒
14^2 = a² + 2*48 + b²⇒
a² + b²=14^2-96=196-96=100
Диагональ d = √(a² + b²) = 10.
Ответ: 10.
32. Параллелограмм ABCD, S = 24, K – середина BC
Площадь ∆ABK равна ¼ площади параллелограмма (основание AB и высота в два раза меньше).
S∆ABK = 24 / 4 = 6.
S_{AKCD} = 24 – 6 = 18.
Ответ: 18.
33. Квадраты, вписанный и описанный вокруг окружности r = √7
• Вписанный: диагональ = 2r ⇒ a = 2r/√2 = √14 ⇒ S₁ = 14.
• Описанный: сторона = 2r ⇒ S₂ = (2√7)² = 28.
Отношение S₁ : S₂ = 1 : 2 (или 0,5).
Ответ: 1 : 2.
34. Дуга L = 9, r = 3
Длина окружности:
C_(окр)=2π r
Длина дуги в радианах
L=C/(2π) * α
α = L/r = 3( рад)
S_(круга)=πr^2
Площадь сектора с дугой в радианах
S_(сектора )=S_(круга)/(2π) * α
S =( ½) r² α = ½ · 9 · 3 = 27/2 = 13,5.
Ответ: 13,5.
35.
Решаем систему двух уравнений:
2x + 5y = 4
x + 2y = 1
умножаем второе уравнение на (-2)
2x + 5y = 4
-2x - 4y =- 2.
Складываем
y = 2 ⇒
Подставляем в уравнение x + 2y = 1
x + 2·2 = 1 ⇒ x = –3.
Ответ: –3.