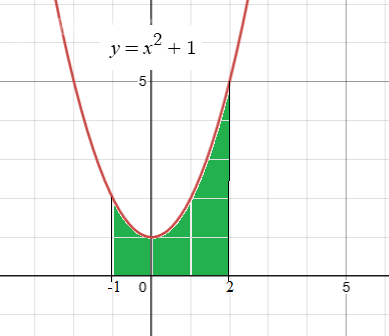
Задача 80453 Вычислить площадь фигуры, ограниченной...

68f7aaef2723c2578435aaf9

10/22/2025 7:56:45 AM

Вычислить площадь фигуры, ограниченной линиями. Решите пожалуйста с чертежом графика

626fab9a354ab65fb2f43abb

10/22/2025 11:13:49 AM

★

Смотрите рисунок. Нужная фигура показана зеленым.
Это криволинейная трапеция.
Чтобы найти ее площадь, нужно взять интеграл.
[m]S=\int \limits_{-1}^{2} (x^2+1)dx = \frac{x^3}{3}+x \bigg |_{-1}^{2} =[/m]
[m]= (\frac{2^3}{3}+2) - (\frac{(-1)^3}{3}-1) = \frac{8}{3}+2+\frac{1}{3}+1 = 6[/m]

Ответ: 6