Задача 80452 соч по алгебре 1 четверть емн...
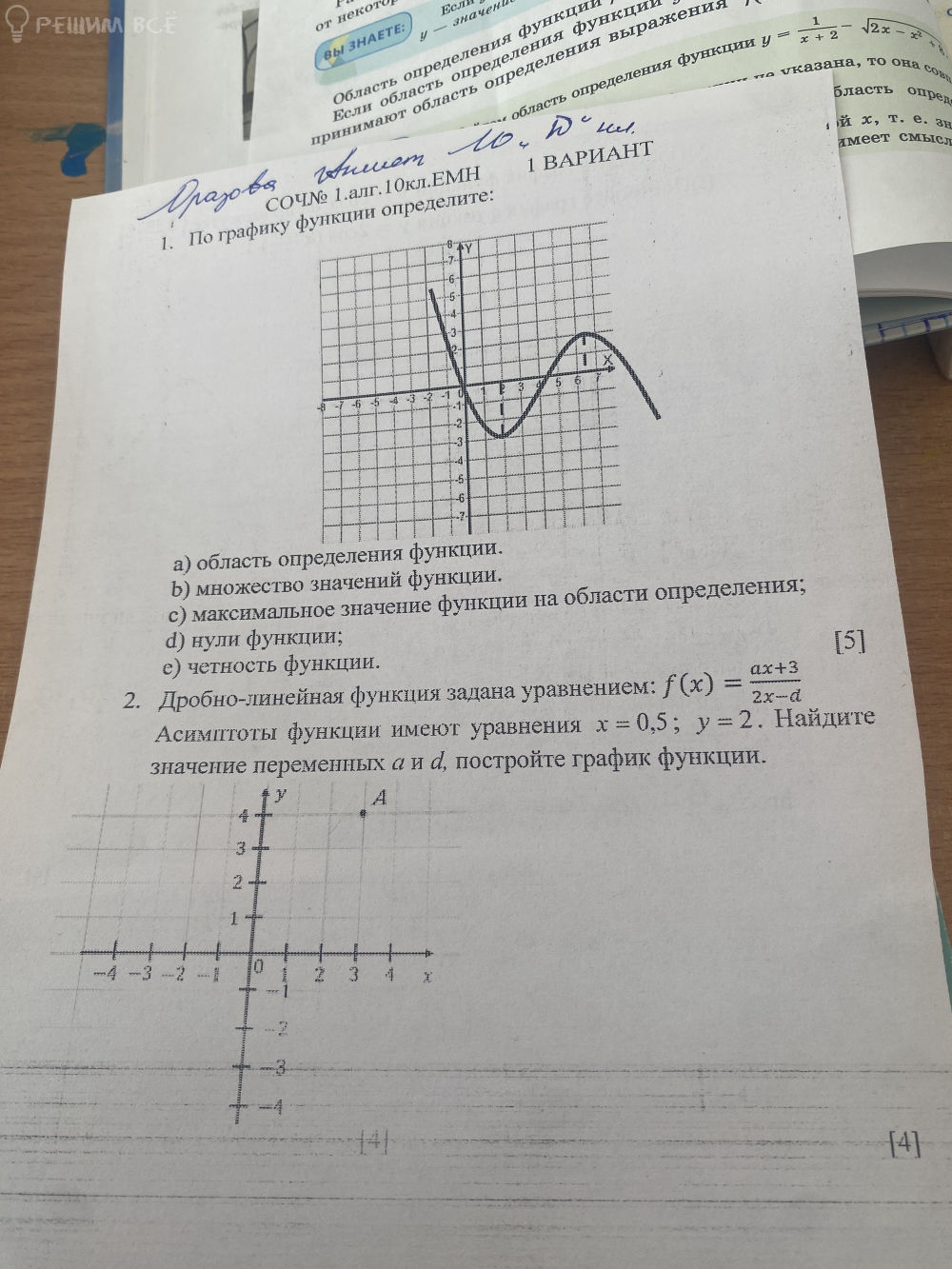
Условие
Решение
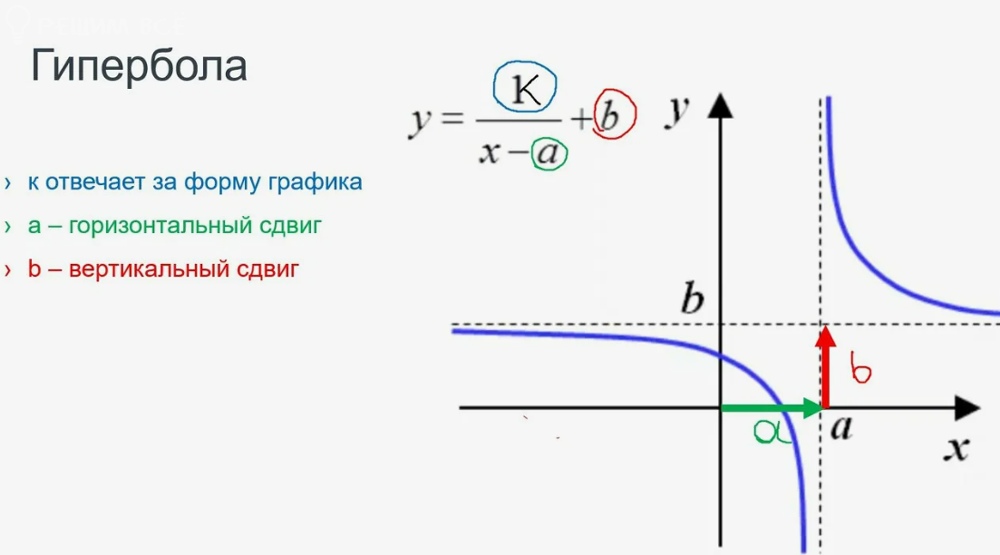
Если заданы асимптоты x=0,5; y=2, то можно написать формулу для указанной дробно-линейной функции:
( см. фото на рис. 3)
[m]y=\frac{k}{x-0,5}+2[/m]
Графику функции принадлежит точка А (3;4) ?
Подставляем ее координаты
[m]4=\frac{k}{3-0,5}+2[/m]
[m]10=k+5[/m]
k=5
[m]y=\frac{5}{x-0,5}+2[/m]
Преобразуем правую часть, приведем к общему знаменателю:
[m]y=\frac{5+2(x-0,5)}{x-0,5}[/m]
[m]y=\frac{5+2(x-0,5)}{x-0,5}[/m]
[m]y=\frac{5+2x-1}{x-0,5}[/m]
[m]y=\frac{2x+4}{x-0,5}[/m]
Умножаем числитель и знаменатель на 2
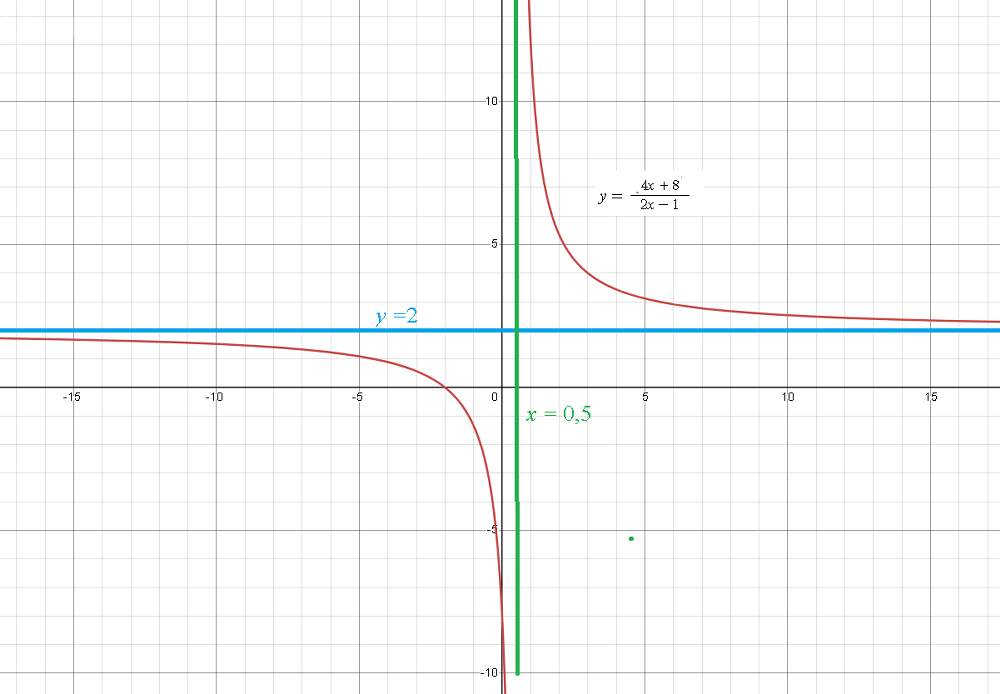
[m]y=\frac{4x+8}{2x-1}[/m]
По условию уравнение функции имеет вид
[m]y=\frac{ax+3}{2x-d}[/m]
Понимаем, что должно быть а= 4; d=1
НО
[m]y=\frac{4x+3}{2x-1}[/m] не проходит через точку (3;4)
Опечатка или ???
и
1 задача задана некорректно.
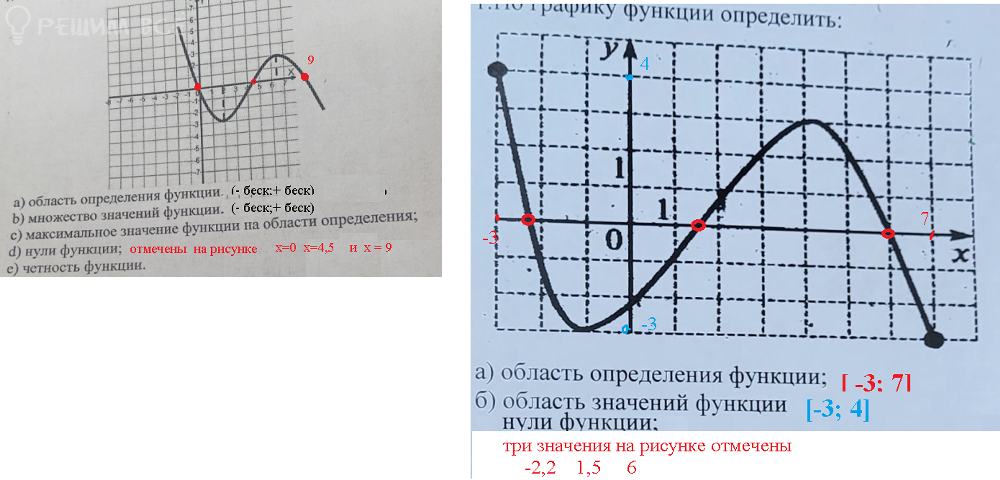
Если это схематический рисунок, то область определения (- ∞ ; + ∞ )
Тогда и область изменения (- ∞ ; + ∞ )
И три нуля: х=0; х=4,5 ; х=9
Функция не является ни четной, ни нечетной ( график не симметричен относительно оси Оу и не симметричен относительно нуля
Нет ни наибольшего, ни наименьшего значения
Если график это только черная линия на рисунке.
Тогда обращаем внимание на крайние точки графика. Их координаты определить можно только приближенно
Обычно крайние точки отмечены жирным кружком или пустым кружком.
( см. рисунок справа)