Задача 80451 ...

626fab9a354ab65fb2f43abb

10/21/2025 11:14:37 PM

★

1) [m]\sqrt[4]{\frac{81}{625}} \cdot \sqrt[3]{4 \frac{17}{27}}+(-3 \sqrt{2})^2 - (-\sqrt[5]{13})^5[/m]
Решаем по действиям:
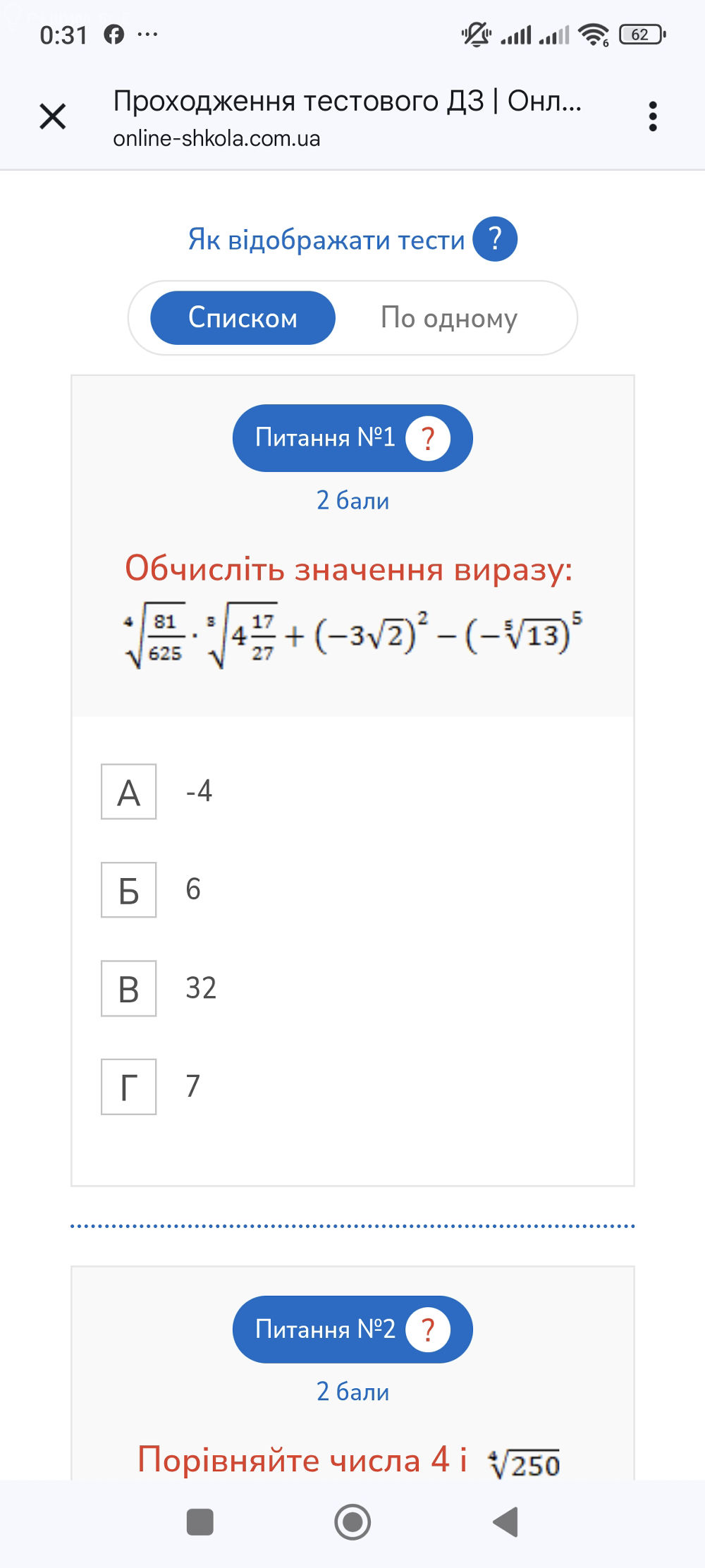
[m]\sqrt[4]{\frac{81}{625}} = \sqrt[4]{\frac{3^4}{5^4}} = \frac{3}{5}[/m]
[m]\sqrt[3]{4 \frac{17}{27}} = \sqrt[3]{\frac{4 \cdot 27+17}{27}} = \sqrt[3]{\frac{125}{27}} = \sqrt[3]{\frac{5^3}{3^3}} = \frac{5}{3}[/m]
[m](-3 \sqrt{2})^2 = (3 \sqrt{2})^2 = 3^2 \cdot 2 = 9 \cdot 2 = 18[/m]
[m](-\sqrt[5]{13})^5 = -(\sqrt[5]{13})^5 = -13[/m]
Получаем:
[m]\frac{3}{5} \cdot \frac{5}{3} + 18 - (-13) = 1+18+13=32[/m]
Ответ: В) 32

2) Сравнить 4 и [m]\sqrt[4]{250}[/m]
Так как [m]4^4 = 256[/m], то [m]4 = \sqrt[4]{256}[/m]
[m]\sqrt[4]{256} > \sqrt[4]{250}[/m]
Ответ: [m]4 > \sqrt[4]{250}[/m]