Задача 80437 П1 П2 П3 П4 П5 П6 П7 П1 11 ...
Условие
П1 11 15 7
П2 11 17 6 12
П3 15 17 6 8
П4 7 6 6
П5 8 9
П6 20 14 8
П7 8
Так как таблицу и схему рисовали независимо друг от друга, нумерация населённых пунктов в таблице никак не связана с
буквенными обозначениями на графе. Известно, что длина дороги DE меньше, чем длина дороги AB. Определите длину дороги
AG. В ответе запишите целое число — длину дороги в километрах.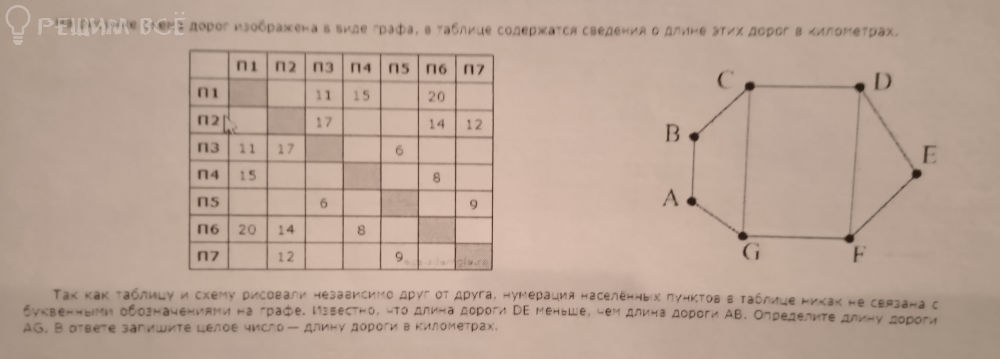
Решение
(просто считаем числа в строке таблицы):
• П1 – 3 дороги • П2 – 3 • П3 – 3
• П4 – 3 • П5 – 2 • П6 – 3 • П7 – 3
В графе только одна вершина имеет степень 2 – это точка A
(она соединена лишь с B и G).
Следовательно
A ≡ П5.
2 . Из П5 выходят две дороги:
П5-П3 = 8 и П5-П7 = 9.
Значит именно эти два пункта – соседи A, то есть B и G.
Разберёмся, кто из них B, а кто G.
3 . У вершины B, помимо дороги к A, есть ещё две – к C и E
(всего 3 дороги).
У вершины G, кроме дороги к A, есть ещё две – к F и D
(тоже 3 дороги).
Посмотрим на связи П3 и П7.
• П3 имеет дороги к П5 (8), к П1 (15) и к П4 (6).
• П7 имеет дороги к П5 (9), к П6 (8) и к П2 (12).
У П3 соседями (кроме П5) являются именно П1 и П4,
которые потом окажутся C и E – как требуется для вершины B.
Следовательно
B ≡ П3, G ≡ П7.
4 . Продолжаем вдоль многоугольника.
B (П3) соединён с C, поэтому C ≡ П1 (длина П3-П1 = 15).
C соединён с D, то есть D ≡ П2 (длина П1-П2 = 11).
Далее D соединён с E, а в таблице П2-П4 = 6,
значит E ≡ П4.
E соединён с F, поэтому F ≡ П6 (длина П4-П6 = 14).
Остаётся проверить, что G (П7) действительно соединён с F и D:
П7-П6 = 8 и П7-П2 = 12 – всё есть в таблице.
Таким образом получили однозначное соответствие
(оно же удовлетворяет условию DE < AB, потому что
DE = П2-П4 = 6 км, а AB = П5-П3 = 8 км).
5 . Нужная дорога – AG.
A ≡ П5, G ≡ П7, длина П5-П7 = 9 км.
Ответ: 9