Задача 80435 ...
Условие
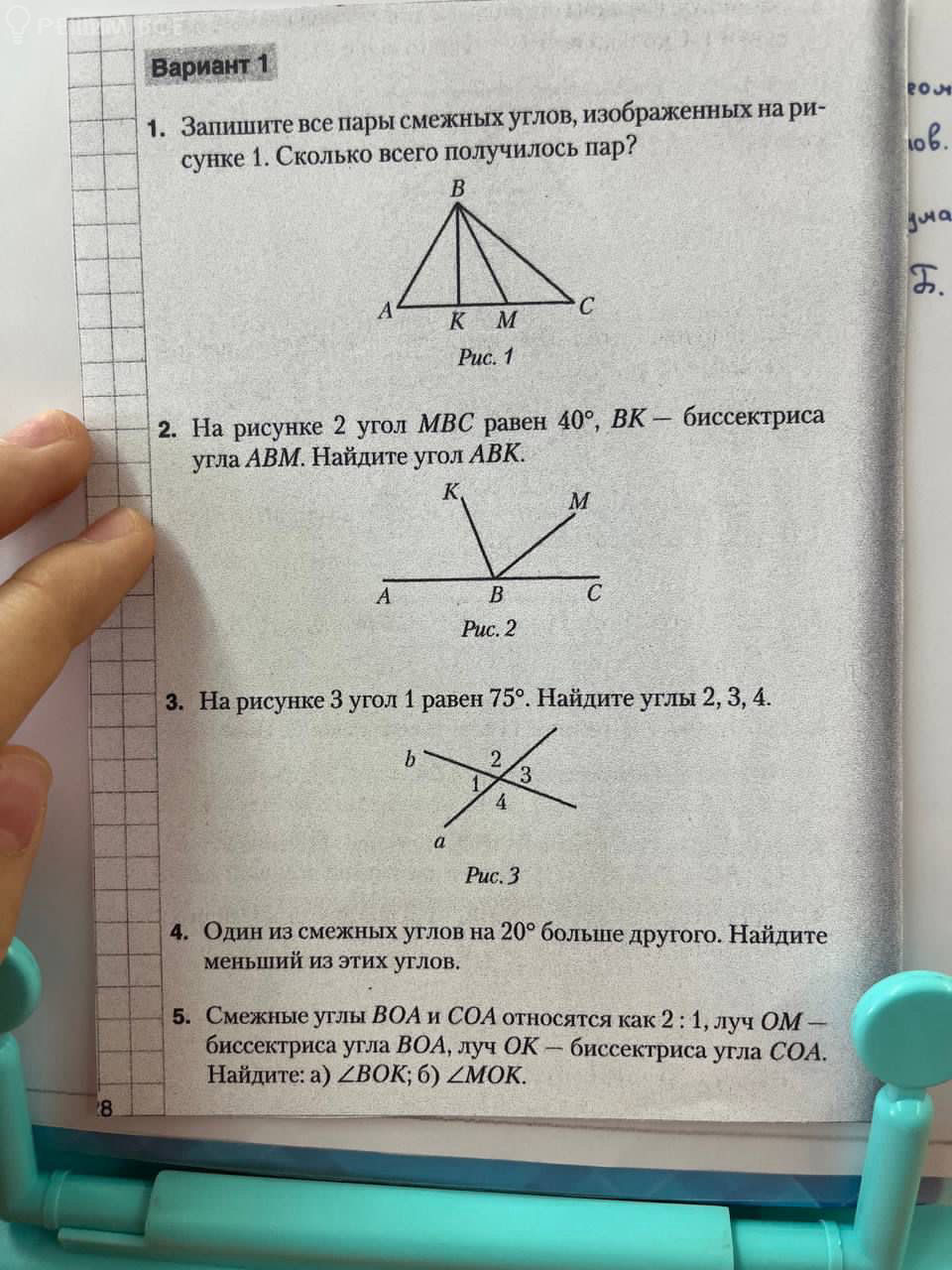
1. Запишите все пары смежных углов, изображенных на рисунке 1. Сколько всего получилось пар?
(Рисунок 1)
2. На рисунке 2 угол MBC равен 40°, BK — биссектриса угла ABM. Найдите угол ABK.
(Рисунок 2)
3. На рисунке 3 угол 1 равен 75°. Найдите углы 2, 3, 4.
(Рисунок 3)
4. Один из смежных углов на 20° больше другого. Найдите меньший из этих углов.
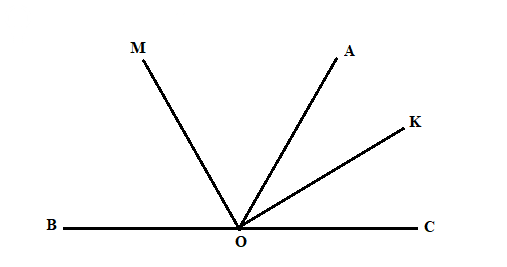
5. Смежные углы BOA и COA относятся как 2 : 1, луч OM — биссектриса угла BOA, луч OK — биссектриса угла COA. Найдите: а) ∠BOK; б) ∠MOK.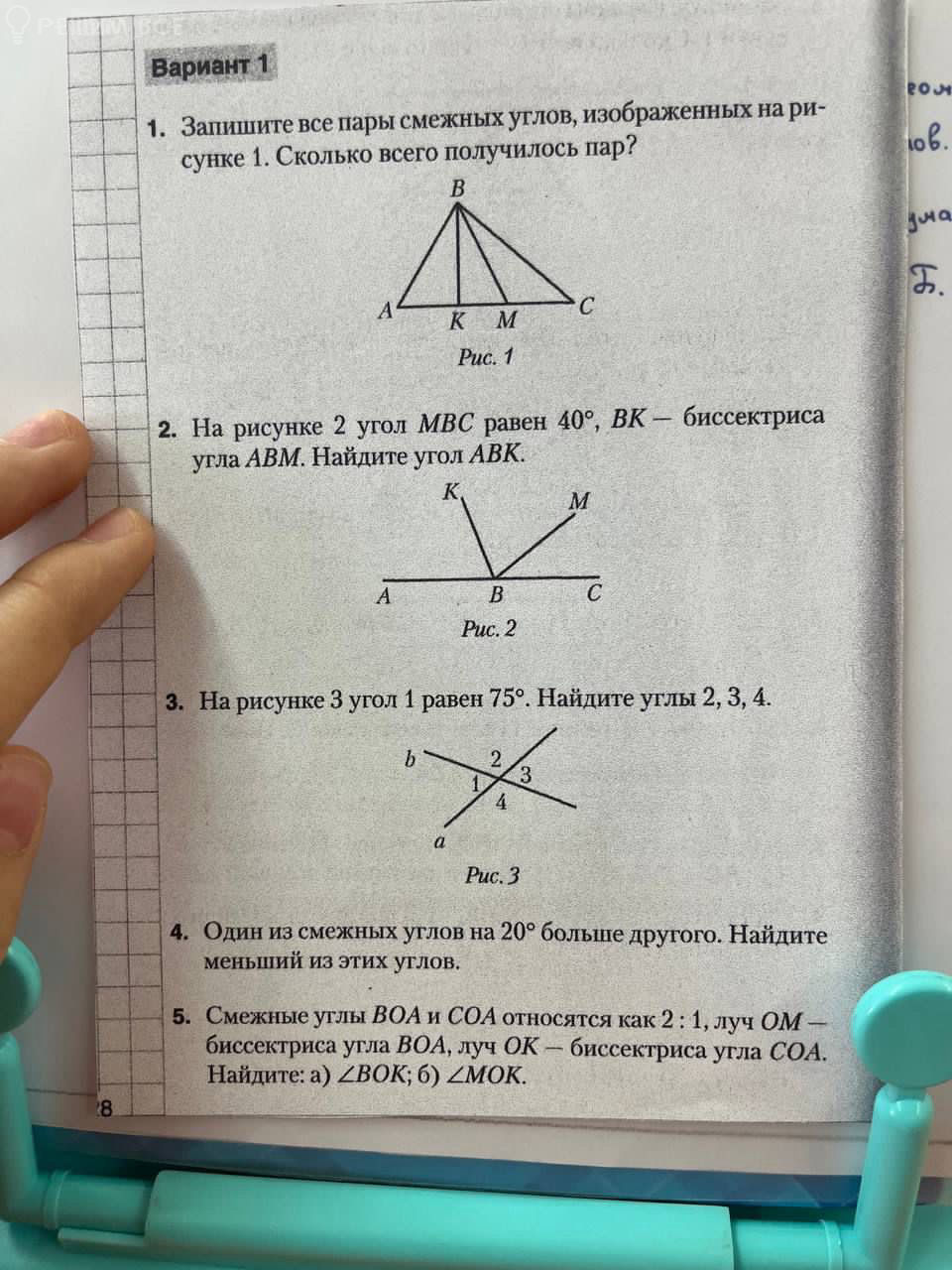
Решение
Сумма двух смежных углов равна 180°.
1) Две пары смежных углов: (BKA, BKM); (BMK, BMC).
2) ABM и MBC - смежные углы, их сумма равна 180°.
Если MBC = 40°, то ABM = 180° - 40° = 140°
BK - биссектриса угла ABM, поэтому:
ABK = KBM = 140°/2 = 70°
3) Смежные углы дают в сумме 180°,
вертикальные углы равны.
Углы ∠ 1 и ∠ 3 - вертикальные, ∠ 2 и ∠ 4 - тоже.
∠ 1 = 75°, ∠ 3 = ∠ 1 = 75°
∠ 2 = ∠ 4 = 180° - ∠ 1 = 180° - 75° = 105°
4) Сумма смежных углов 180°, а разность равна 20°.
Чтобы найти меньший угол, нужно из суммы углов вычесть их разность, а результат разделить пополам.
180° - 20° = 160°
160° : 2 = 80° - это меньший угол.
180° - 80° = 100° - это больший угол.
5) Смотрите рисунок.
Если BOA : COA = 2 : 1, то COA = x, BOA = 2x
Так как они смежные, то их сумма равна 180°
BOA + COA = 180°
2x + x = 180°
x = COA = 60°
2x = BOA = 120°
Так как OM - биссектриса BOA, то
BOM = AOM = BOA/2 = 120°/2 = 60°
Так как OK - биссектриса COA, то
COK = AOK = AOM/2 = 60°/2 = 30°
а) BOK = BOA + AOK = 120° + 30° = 150°
б) MOK = AOM + AOK = 60° + 30° = 90°