Задача 80415 Радиус вписанной в основание окружности...
Условие
Решение
Основание правильной 4-угольной пирамиды - это квадрат.
Если радиус вписанной в квадрат окружности равен 6, то сторона квадрата равна диаметру, то есть 12.
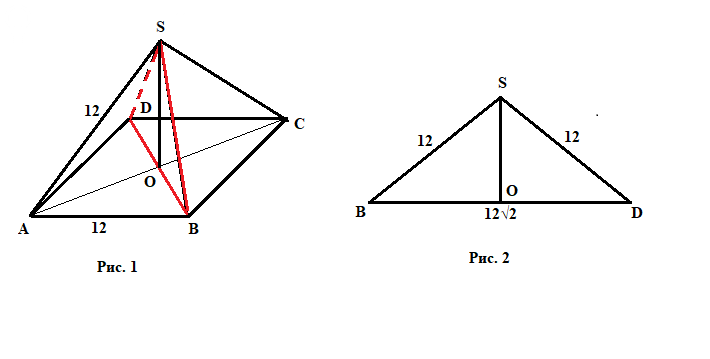
Диагональное сечение пирамиды BDS - это равнобедренный треугольник, основание которого - это диагональ квадрата BD.
a = BD = 12sqrt(2)
А боковые стороны - это боковые ребра пирамиды.
Так как пирамида правильная, то считаем, что боковые ребра равны стороне основания, то есть
b = BS = DS = 12.
Надо найти площадь этого треугольника.
Можно найти по формуле Герона, зная три стороны, но она достаточно сложная.
Проще найти высоту SO. Смотрите рисунок 2.
Треугольник BSO - прямоугольный.
BO = DO = BD/2 = 12sqrt(2)/2 = 6sqrt(2)
По теореме Пифагора:
SO^2 = BS^2 - BO^2 = 12^2 - (6sqrt(2))^2 =
= 144 - 36*2 = 144 - 72 = 72
h = SO = sqrt(72) = 6sqrt(2)
S(BDS) = a*h/2 = 12sqrt(2)*6sqrt(2)/2 = 12*6*2/2 = 72
Ответ: 72