Задача 80404 Задание 3. Проверить совместность...
Условие
совместности решить её:
а) по формулам Крамера;
методом Гаусса; в) матричным
способом.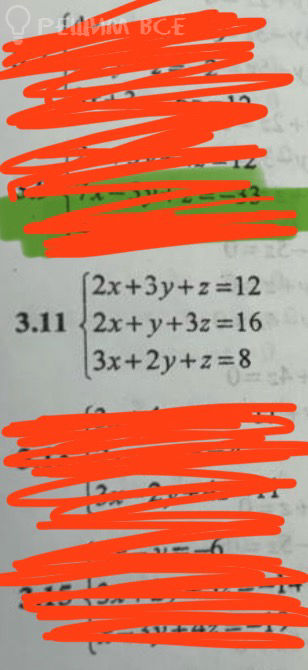
Решение
{ 2x + y + 3z = 16
{ 3x + 2y + z = 8
Умножаем уравнения так, чтобы коэффициенты при x были одинаковые, но с разными знаками.
1 уравнение умножаем на 3, 2 уравнение умножаем на -3,
3 уравнение умножаем на -2.
{ 6x + 9y + 3z = 36
{ -6x - 3y - 9z = -48
{ -6x - 4y - 2z = -16
Складываем 1 и 2 уравнение и 1 и 3 уравнение.
{ 6x + 9y + 3z = 36
{ 0x + 6y - 6z = -12
{ 0x + 5y + z = 20
2 уравнение делим на 6.
{ 6x + 9y + 3z = 36
{ 0x + y - z = -2
{ 0x + 5y + z = 20
Складываем 2 и 3 уравнение.
6y = 18
y = 3
Это совместное уравнение.
Продолжаем решать методом Гаусса.
Из 2 уравнения:
z = y + 2 = 3 + 2 = 5
Подставляем y и z в 1 уравнение.
6x + 9*3 + 3*5 = 36
6x + 27 + 15 = 36
6x = 36 - 27 - 15
6x = -6
x = -1
Ответ: (-1; 3; 5)
Методом Крамера. Находим матрицы:
[m]\Delta = \begin{vmatrix}
2 & 3 & 1 \\
2 & 1 & 3 \\
3 & 2 & 1 \\
\end{vmatrix} = [/m]
= 2*1*1 + 2*2*1 + 3*3*3 - 1*1*3 - 1*2*3 - 2*3*2 =
= 2 + 4 + 27 - 3 - 6 - 12 = 12
[m]\Delta(x) = \begin{vmatrix}
12 & 3 & 1 \\
16 & 1 & 3 \\
8 & 2 & 1 \\
\end{vmatrix} = [/m]
= 12*1*1 + 16*2*1 + 3*3*8 - 1*1*8 - 1*16*3 - 12*3*2 =
= 12 + 32 + 72 - 8 - 48 - 72 = -12
[m]\Delta(y) = \begin{vmatrix}
2 & 12 & 1 \\
2 & 16 & 3 \\
3 & 8 & 1 \\
\end{vmatrix} = [/m]
= 2*16*1 + 2*8*1 + 3*3*12 - 1*16*3 - 1*2*12 - 8*3*2 =
= 32 + 16 + 108 - 48 - 24 - 48 = 36
[m]\Delta(z) = \begin{vmatrix}
2 & 3 & 12 \\
2 & 1 & 16 \\
3 & 2 & 8 \\
\end{vmatrix} = [/m]
= 2*1*8 + 2*2*12 + 3*3*16 - 12*1*3 - 8*2*3 - 2*16*2 =
= 16 + 48 + 144 - 36 - 48 - 64 = 60
Решение:
[m]\large x = \frac{\Delta(x)}{\Delta} = \frac{-12}{12} = -1[/m]
[m]\large y = \frac{\Delta(y)}{\Delta} = \frac{36}{12} = 3[/m]
[m]\large z = \frac{\Delta(z)}{\Delta} = \frac{60}{12} = 5[/m]