Задача 80355 Все стороны равносторонней трапеции с...
Условие
По возможности с фотографией.
Решение
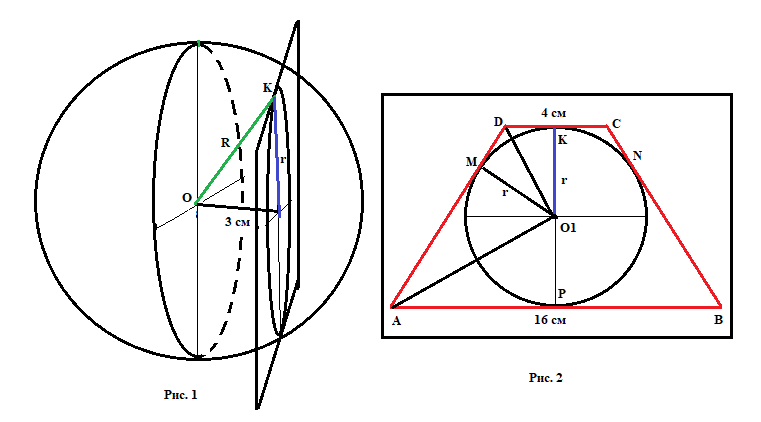
На Рис. 1 показан шар и плоскость, на которой находится трапеция. Сама трапеция не показана, там очень большие искажения, трудно нарисовать. Только сечение малым кругом.
Осевое сечение шара показано большим кругом.
Расстояние от осевого сечения до плоскости трапеции 3 см.
На Рис. 2. Показана сама трапеция. Окружность, вписанная в трапецию - это сечение шара.
У трапеции основания равны 4 см и 16 см, и она равнобочная.
Не равносторонняя! Равносторонняя трапеция - это трапеция, у которой боковые стороны равны меньшему основанию.
Но, если эти стороны все равны по 4 см, то нижнее основание не может быть равно 16 см, оно должно быть меньше, чем
3*4 = 12 см.
Найти: радиус шара R. Он показан слева зеленым.
Решение.
Нам нужно найти радиус малого сечения r, он показан синим.
Как известно, если из одной точки, например, из вершины A трапеции, проведено две касательных к окружности, то эти длины равны.
AM = AP = BN = BP = 16/2 = 8 см.
CN = CK = DM = DK = 4/2 = 2 см.
Боковая сторона AD = BC = 8 + 2 = 10 см.
Заметим, что сумма углов PAM + MDK = 180°
(смежные углы трапеции).
А углы O1AM = PAM/2; MDO1 = MDK/2, значит:
O1AM + MDO1 = (PAM + MDK)/2 = 180°/2 = 90°
Отсюда угол AO1D = 90°
По теореме Пифагора можно написать такие равенства:
AM^2 + MO1^2 = AO1^2
DM^2 + MO1^2 = DO1^2
AO1^2 + DO1^2 = AD^2
Подставляем 1 и 2 уравнения в 3 уравнение:
AM^2 + MO1^2 + DM^2 + MO1^2 = AD^2
Заменяем названия сторон их значениями:
8^2 + r^2 + 2^2 + r^2 = 10^2
64 + 4 + 2r^2 = 100
2r^2 = 32
r^2 = 16
r = 4 см
Теперь обратимся опять к Рис. 1.
Мы видим, что два радиуса R и r, а также расстояние между центрами кругов OO1, образуют прямоугольный треугольник.
O1K^2 + OO1^2 = OK^2
r^2 + 3^2 = R^2
16 + 9 = R^2
R = 5 см
Ответ: 5 см