Задача 8035 Наклонная крыша установлена на трёх...
Условие
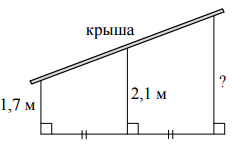
математика 8-9 класс
21713
Решение
(x+1,7)/2 = 2,1
x+1,7 = 4,2
x = 4,2-1,7 = 2,5
Ответ: 2,5

(x+1,7)/2 = 2,1
x+1,7 = 4,2
x = 4,2-1,7 = 2,5
Ответ: 2,5