Задача 80295 ...

66758a5f4a6eb928f58e676d

6/26/2025 10:15:02 AM

26) Груз массой M = 800 г соединён невесомой и нерастяжимой нитью, перекинутой через гладкий невесомый блок, с бруском массой m = 400 г. К этому бруску на лёгкой пружине жёсткостью k = 80 Н/м подвешен второй такой же брусок.
Длина нерастянутой пружины l = 10 см, коэффициент трения груза о поверхность стола μ = 0,2. Определите длину пружины при движении брусков, считая, что при этом движении она
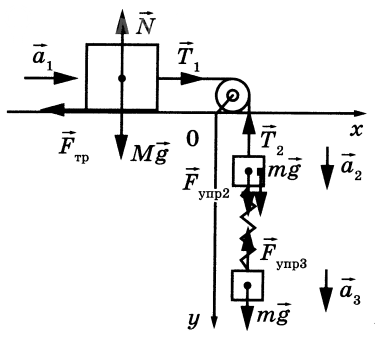
постоянна. Сделайте рисунок с указанием сил, действующих на груз и бруски. Обоснуйте применимость используемых законов к решению задачи.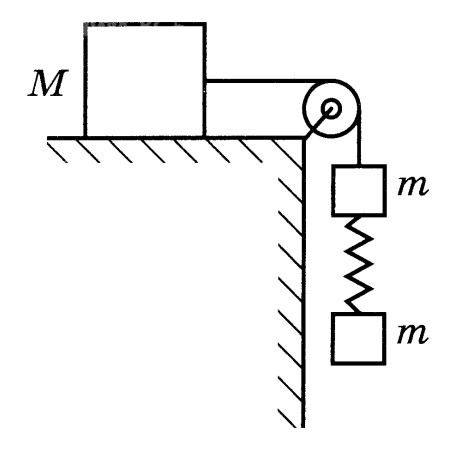

68501b46d00c766c9c688611

6/26/2025 10:15:46 AM

★

Решение выполняем по второму закону Ньютона для каждого из трёх тел,
принимая направление движения за положительное
(груз М – вправо, бруски m – вниз).
Обозначения
a – общее ускорение системы,
T – натяжение нити,
F = k x – сила упругости пружины, x – её удлинение,
l = 10 см – естественная длина пружины,
μ = 0,20 – коэффициент трения,
k = 80 Н/м – жёсткость пружины,
m = 0,40 кг, M = 0,80 кг, g = 9,8 м/с².

1. Груз M на столе

Силы: T (вправо), сила трения R = μMg (влево).
M a = T – R.  (1)

2. Верхний брусок m (привязан к нити)

Силы вниз: mg и F; вверх: T.
m a = mg + F – T.  (2)

3. Нижний брусок m (подвешен на пружине)

Силы вниз: mg; вверх: F.
m a = mg – F.  (3)

(Условие «длина пружины постоянна» означает, что оба бруска имеют
одинаковое ускорение, т. е. относительного движения между ними нет.)

Из (3): F = m(g – a).  (4)

Подставляем (4) в (2):

m a = mg + m(g – a) – T
2m a = 2mg – T ⇒ T = 2mg – 2m a.  (5)

Подставляем (5) в (1):

M a = (2mg – 2m a) – R
(M + 2m) a = 2mg – R
a = (2mg – R)/(M + 2m).

Численно

R = μMg = 0,2·0,80·9,8 ≈ 1,568 Н
2mg = 2·0,40·9,8 = 7,84 Н
M + 2m = 0,80 + 0,80 = 1,60 кг

a = (7,84 – 1,568)/1,60 ≈ 3,92 м/с².

Сила упругости (4):

F = m(g – a)=0,40·(9,8 – 3,92)=0,40·5,88=2,352 Н.

Удлинение пружины

x = F/k = 2,352 Н / 80 Н/м ≈ 0,0294 м ≈ 2,94 см.

Длина пружины в движении

L = l + x ≈ 10 см + 2,94 см ≈ 12,9 см.

Ответ: пружина имеет длину ≈ 13 см (точнее 12,9 см).

Почему законы применимы
• Система рассматривается как совокупность материальных точек;
• нить и блок невесомы и нерастяжимы → натяжение одинаково;
• трение на столе кинетическое, сила R = μMg постоянна;
• деформации пружины малы, выполняется закон Гука;
• относительного движения между брусками нет ⇒ их ускорения одинаковы, что позволило использовать одну неизвестную a и считать длину пружины постоянной.