Задача 80195 ...
Условие
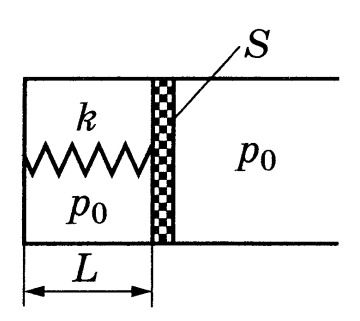
Решение
Vi = SL – начальный объём газа,
Vf = S(L + b) – конечный объём,
x – удлинение пружины.
1. Связь давления в процессе
В любой момент времени
p = p0 + Fs / S = p0 + kx / S, (1)
где x – текущее удлинение пружины (х = 0 в начале, х = b в конце).
2. Работу газа найдём через интеграл
A = ∫ p dV = ∫0b (p0 + kx/S) S dx
= ∫0b (p0 S + kx) dx
= p0 S b + ½ k b². (2)
3. Из уравнения состояния ideal-газа
nRTi = p0Vi = p0SL,
nRTf = pfVf = (p0 + kb/S) S (L + b)
= p0S(L + b) + k b (L + b). (3)
4. Приращение внутренней энергии одноатомного газа
ΔU = (3/2) nR (Tf – Ti)
= (3/2) [pfVf – p0Vi]
= (3/2) [p0S b + k b (L + b)]. (4)
5. Первый закон термодинамики
Q = ΔU + A. Подставляя (2) и (4):
Q = (3/2)[p0 S b + k b (L + b)] + p0 S b + ½ k b²
= (5/2) p0 S b + k b[(3/2) L + 2 b]. (5)
6. Выразим жёсткость пружины k:
k = [Q – (5/2) p0 S b] / [b((3/2) L + 2 b)]
= (2Q – 5 p0 S b) / [b (3 L + 4 b)]. (6)
Ответ
Жёсткость пружины равна
k = (2Q − 5 p₀ S b) / [b (3L + 4b)].