Задача 80148 ...
Условие
Обсудите применимость законов, используемых для решения задачи.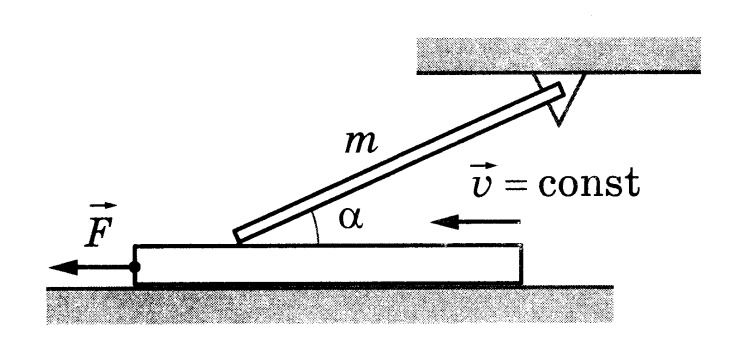
Решение
Доска движется без ускорения, следовательно
F – f = 0 ⇒ f = F = 2 Н.
Сила трения, действующая на стержень, по модулю такая же, но направлена влево.
2. Равновесие стержня
Стержень покоится ⇒ ΣF = 0, ΣM(верхний шарнир)=0.
а) Сумма моментов относительно шарнира (z-ось «из страницы» положительна при противо-часовой вращении).
Для однородного стержня длиной L
– момент веса: τg = (L/2) mg cosα (против часовой, «+»);
– момент трения: τf = – L f sinα (по часовой);
– момент нормальной реакции: τN = – L N cosα (по часовой).
Στ = 0 ⇒ (L/2)mg cosα – L f sinα – L N cosα = 0
деля на L cosα:
mg /2 – f tanα – N = 0 ⇒ N = mg/2 – f tanα. (1)
б) Условие трения
Для покоя соприкасающихся поверхностей |f| ≤ μN.
Чтобы сила трения могла равняться 2 Н, нужен минимум
N = f / μ = 2 / 0.20 = 10 Н. (2)
3. Масса стержня
Подставляем (2) в (1):
10 = mg/2 – 2 tan30°
tan30° = 1/√3 ≈ 0.577
mg/2 = 10 + 2·0.577 ≈ 11.155 Н
m = 2·11.155 / g ≈ 22.31 / 9.8 ≈ 2.3 кг.
Ответ: m ≈ 2,3 кг (при g = 9,8 м/с²; при g = 10 м/с² – около 2,2 кг).
Применимость используемых законов
• Рассмотрена система в лабораторной (почти инерциальной) системе отсчёта, т.к. доска и стержень движутся без ускорения – условия статического равновесия (ΣF = 0, ΣM = 0) применимы.
• Стержень считается жёстким, однородным, его масса распределена равномерно.
• Принята модель сухого трения Кулона–Амонтона (|f| ≤ μN); коэффициент μ=0,2 задан.
• Трением шарнира и опор доски пренебрегаем, как указано в условии, поэтому дополнительных сил нет.
• Движение доски равномерное, поэтому наличие или отсутствие её инерционной массы на равновесие сил не влияет; достаточно, чтобы внешняя сила F уравновешивалась трением.