Задача 80051 ...

66758a5f4a6eb928f58e676d

6/24/2025 1:53:10 PM

26) На горизонтальном неподвижном столе лежит доска, на которой находится маленький брусок массой т = 400 г. Брусок и доска связаны невесомой нерастяжимой нитью, перекинутой через невесомый блок, закреплённый на стене (отрезки нити, не лежащие на блоке, горизонтальны и параллельны). Коэффициент трения между бруском и доской μ₁ = 0,5, между столом и доской μ₂ = 0,3. Доску тянут вправо постоянной горизонтальной силой F, параллельной горизонтальным отрезкам нити, F = 12 Н. Чему равна масса доски М, если модуль ускорения бруска относительно стола a = 2 м/с²? Трением в оси блока пренебречь. Сделайте рисунок с указанием сил, действующих на доску и брусок.

Обсудите применимость законов, используемых для решения задачи.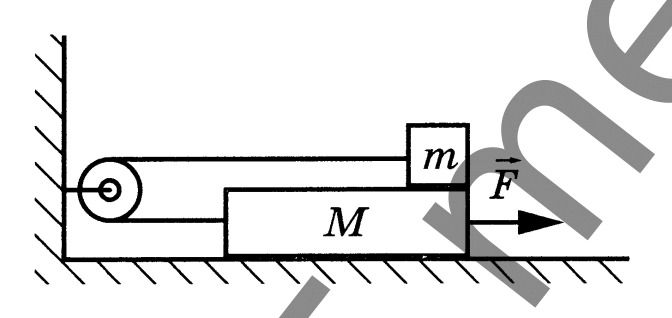

68501b46d00c766c9c688611

6/24/2025 1:59:21 PM

★

Решение приведём в системе отсчёта, связанной со столом (она инерциальна, так как стол неподвижен). Ось ОХ направим вправо.

1. Кинематическая связь “доска-нить-блок”.
Концы нити прикреплены к доске и к бруску, а сама нить переброшена через неподвижный блок на стене.
При смещении доски вправо на хD длина правого горизонтального участка нити увеличивается на хD. Чтобы общая длина нити не изменилась, левый горизонтальный участок должен укоротиться на ту же величину, т.е. брусок смещается влево на хB = –хD.
Отсюда для ускорений:

aD + aB = 0 → aD = –aB.

По условию величина ускорения бруска относительно стола |aB| = 2 м/с².
Значит

aB = –2 м/с² (влево), aD = +2 м/с² (вправо).

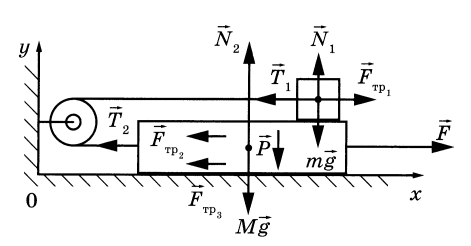
2. Силы (см. рисунок).

На брусок m = 0,40 кг действуют
– сила натяжения нити T (влево);
– сила трения скольжения со стороны доски f₁ = μ₁m g (вправо, так как относительное скольжение бруска по доске – влево);
– веса и нормальные реакции, взаимно компенсирующиеся по вертикали.

На доску массой М действуют
– заданная сила F = 12 Н (вправо);
– сила натяжения той же нити T (влево);
– сила трения со стороны бруска –f₁ (влево);
– сила трения между доской и столом
f₂ = μ₂ (M + m) g (влево: доска скользит вправо).

3. Уравнения динамики (II закон Ньютона).

Для бруска:

m aB = f₁ – T. (1)

Для доски:

M aD = F – T – f₁ – f₂. (2)

4. Численные величины при g = 9,8 м/с²

f₁ = μ₁ m g = 0,5·0,40·9,8 ≈ 1,96 Н,
m aB = 0,40·(–2) = –0,80 Н.

Из (1) получаем натяжение нити

–0,80 = 1,96 – T ⇒ T ≈ 2,76 Н.

Сила трения доска-стол:

f₂ = μ₂ (M + m) g = 0,30·(M + 0,40)·9,8 = 2,94 (M + 0,40) Н.

Подставляя всё в (2) и учитывая aD = +2 м/с²:

2M = 12 – 2,76 – 1,96 – 2,94 (M + 0,40).

2M = 7,28 – 2,94M – 1,176 = 6,104 – 2,94M.

4,94M = 6,104 ⇒ M ≈ 1,24 кг.

При округлении до двух значащих цифр:

M ≈ 1,2 кг.

Ответ: масса доски М ≈ 1,2 кг.