Задача 79989 Три прямые AВ, CD, MN пересекаются в...
Условие
1) угол COM = угол A0C + угол MOB;
2) угол AOM = 135°, OВ - биссектриса угла MOD.
* Пункты 1) и 2) решать независимо друг от друга.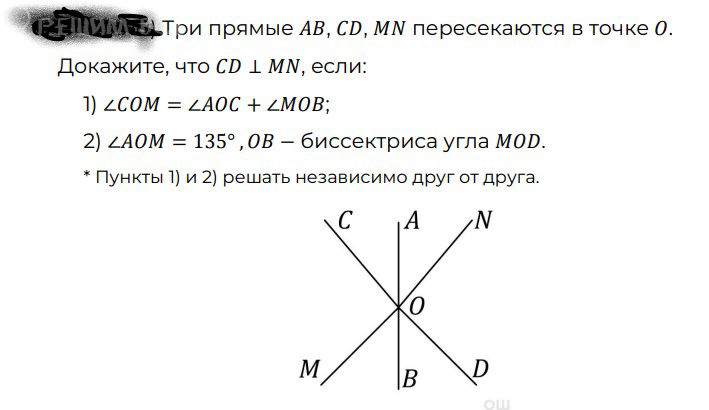
Решение
∠ AOC + ∠ COM + ∠ MOB = ∠ AOB = 180° (развернутый угол)
Если ∠ COM = ∠ AOC + ∠ MOB, то получаем:
∠ COM + (∠ AOC + ∠ MOB) = 180°
∠ COM + ∠ COM = 180°
∠ COM = 90°
Значит, CD ⊥ MN
2) ∠ AOM = 135°, OB - биссектриса угла ∠ MOD
Пусть величина угла ∠ MOD = 2α, тогда ∠ MOB = ∠ BOD = α
∠ BOD и ∠ AOC - вертикальные углы, они равны.
∠ AOC = ∠ MOB = ∠ BOD = α
Теперь получаем систему:
{ ∠ AOM = 135°
{ ∠ AOM + ∠ MOB = 180°
Подставляем 1 уравнение во 2 уравнение.
В 1 уравнении заменяем ∠ AOM = ∠ AOC + ∠ COM:
{ ∠ AOC + ∠ COM = 135°
{ 135° + α = 180°
Отсюда:
{ α = 45°
{ ∠ AOC + ∠ COM= 135°
Но ∠ AOC = α, поэтому получаем:
α + ∠ COM = 135°
∠ COM = 90°
Значит, CD ⊥ MN