Задача 79987 ...

66758a5f4a6eb928f58e676d

6/21/2025 5:15:44 PM

24) В качестве рабочего тела в тепловой машине используется идеальный одноатомный газ, который совершает циклический процесс, состоящий из изобарного нагревания (1→2), изохорного охлаждения (2→3) и адиабатного сжатия (3→1). Известно, что работа, совершённая газом в изобарном процессе, в 4 раза больше работы, совершённой над газом при адиабатном сжатии. Определите КПД этой тепловой машины.

68501b46d00c766c9c688611

6/21/2025 5:46:18 PM

★

Обозначим состояния газа величинами
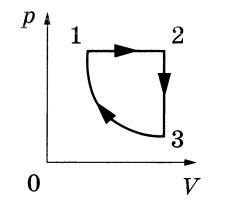
p₁,V₁,T₁ – в начале цикла (точка 1),
p₂,V₂,T₂ – после изобарного нагревания (точка 2),
p₃,V₃,T₃ – после изохорного охлаждения (точка 3).

Пусть во время изобарного процесса объём увеличился k-раз:
V₂ = V₃ = kV₁ (k>1).

1. Изобарное нагревание 1→2
 Работа газа
  W₁₂ = p₁( V₂ − V₁ ) = p₁V₁(k−1).
 Используя уравнение Менделеева-Клапейрона p₁V₁ = nRT₁, получаем
  W₁₂ = nRT₁ (k − 1).  (1)

2. Изохорное охлаждение 2→3
 Работы нет (W₂₃ = 0).
 Температура падает от T₂ до T₃, причём при неизменном объёме
  T₂ : T₃ = p₂ : p₃.

3. Адиабатное сжатие 3→1
 Для адиабаты TV^{γ−1}=const ⇒ T₃V₃^{γ−1}=T₁V₁^{γ−1}.
 У одноатомного газа γ = 5/3, поэтому
  T₃ = T₁ / k^{γ−1} = T₁ / k^{2/3}.  (2)

 Работа (работа газа отрицательна, поэтому берём её со знаком «−»):
  W₃₁ = −ΔU₃₁ = −(3/2)nR( T₁ − T₃ ).  (3)

4. Условие задачи
 По условию |W₃₁| = ¼ W₁₂, т.е. W₁₂ = −4 W₃₁.
 Подставляя (1) и (3) и учитывая (2):

 nRT₁(k − 1) = 4·(3/2)nR( T₁ − T₃ )
 k − 1 = 6 ( 1 − T₃/T₁ ) = 6( 1 − k^{−2/3} ).  (4)

5. КПД цикла
 Теплота, полученная газом, вносится только в процессе 1→2:
 Q₁₂ = ΔU₁₂ + W₁₂ = (3/2)nR(T₂ − T₁) + nRT₁(k−1)
    = (3/2)nRT₁(k−1) + nRT₁(k−1) = (5/2)nRT₁(k−1).  (5)

 Полная работа цикла
 W = W₁₂ + W₂₃ + W₃₁ = W₁₂ + W₃₁
  = nRT₁(k−1) − (3/2)nR(T₁ − T₃).
 Но из условия W₁₂ = 4|W₃₁| ⇒ W = 3|W₃₁| = 3·(3/2)nR( T₁ − T₃ ).
 Используя (2):
  W = (9/2)nRT₁(1 − k^{−2/3}).  (6)

 КПД η = W / Q_in. Подставляя (5) и (6):

 η = [ (9/2)nRT₁(1 − k^{−2/3}) ] / [ (5/2)nRT₁(k−1) ]
   = (9/5) · (1 − k^{−2/3})/(k − 1).

 Согласно (4): k−1 = 6(1 − k^{−2/3}); значит

 (1 − k^{−2/3})/(k − 1) = 1/6.

 Следовательно

 η = (9/5) · 1/6 = 9 / 30 = 3 / 10 = 0,30.

Ответ: КПД тепловой машины η = 30 %.