Задача 79985 22) В стакан налита ртуть, а поверх неё...
Условие
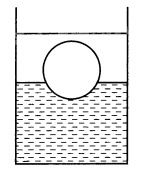
Решение
V – полный объём шара,
V₁ – объём его части, погружённой в ртуть,
V₂ – объём части, находящейся в воде.
Шар плавает, поэтому выполняется условие равновесия сил тяжести и выталкивания (закон Архимеда):
ρFe g V = ρHg g V₁ + ρw g V₂.
Считаем, что шар полностью покрыт жидкостями (над верхней точкой шара ещё есть слой воды), т.е.
V₁ + V₂ = V.
Подставляя V₂ = V − V₁, получаем
ρFe V = ρHg V₁ + ρw (V − V₁)
ρFe V = ρw V + (ρHg − ρw) V₁.
Отсюда доля объёма шара, оказавшегося в ртути,
V₁ / V = (ρFe − ρw) / (ρHg − ρw).
Подставляем плотности (кг/м³):
ρFe ≈ 7.8 × 10³,
ρHg ≈ 13.6 × 10³,
ρw = 1.0 × 10³.
V₁ / V = (7.8 − 1.0) / (13.6 − 1.0) = 6.8 / 12.6 ≈ 0.54.
Ответ: примерно 54 % объёма шара находится в ртути.