Задача 79940 Нужно решить задачу 469...
Условие
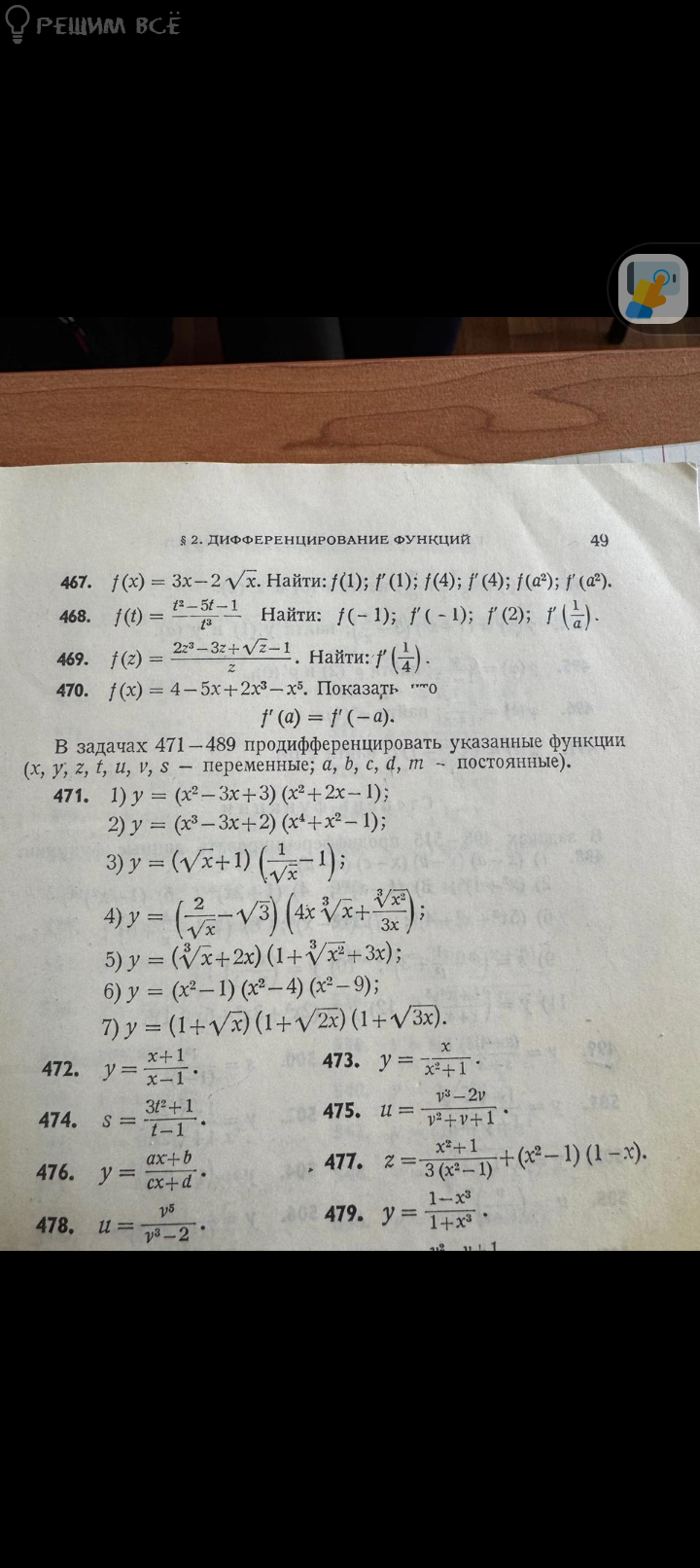
28
Решение
★
[m]\large f'(z) = \frac{(2z^3 - 3z + \sqrt{z} - 1)' z - (2z^3 - 3z + \sqrt{z} - 1) z'}{z^2} = \frac{(6z^2 - 3 + \frac{1}{2\sqrt{z}}) z - (2z^3 - 3z + \sqrt{z} - 1)}{z^2} =[/m]
[m]\large = \frac{6z^3 - 3z + \frac{\sqrt{z}}{2} - 2z^3 +3z - \sqrt{z} + 1}{z^2} = \frac{4z^3 - \frac{\sqrt{z}}{2} + 1}{z^2}[/m]
[m]\large f'(\frac{1}{4}) = \frac{4(1/4)^3 - \frac{\sqrt{1/4}}{2} + 1}{(1/4)^2} = 4^2 \cdot (\frac{1}{4^2} - \frac{1/2}{2} + 1) =[/m]
[m]= 16 \cdot (\frac{1}{16} - \frac{1}{4} + 1) = 1 - 4 + 16 = 13[/m]