Задача 79935 Нужно решить задачу номер 5,6,7,8...
Условие
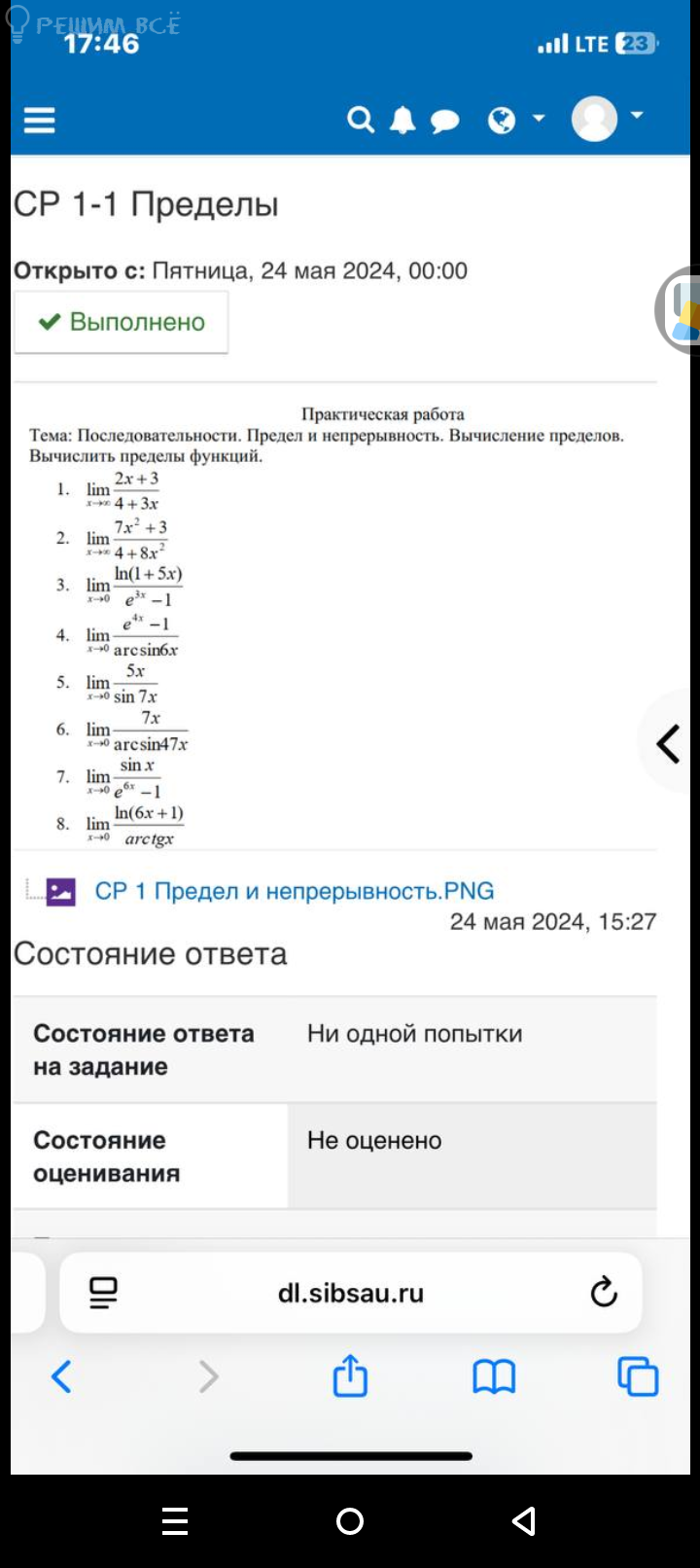
Решение
1 Замечательный предел:
[m]\lim \limits_{t \to 0} \frac{\sin t}{t} = 1[/m]
Поэтому:
[m]\lim \limits_{x \to 0} \frac{5x}{\sin 7x} = \lim \limits_{x \to 0} \bigg (\frac{7x}{\sin 7x} \cdot \frac{5x}{7x} \bigg ) = 1 \cdot \lim \limits_{x \to 0} \frac{5x}{7x} = \frac{5}{7}[/m]
6) [m]\lim \limits_{x \to 0} \frac{7x}{arcsin\ 47x}[/m]
Следствие из 1 Замечательного предела:
[m]\lim \limits_{t \to 0} \frac{arcsin\ t}{t} = 1[/m]
Поэтому:
[m]\lim \limits_{x \to 0} \frac{7x}{arcsin\ 47x} = \lim \limits_{x \to 0} \bigg (\frac{47x}{arcsin\ 47x} \cdot \frac{7x}{47x} \bigg ) = 1 \cdot \lim \limits_{x \to 0} \frac{7x}{47x} = \frac{7}{47}[/m]
7) [m]\lim \limits_{x \to 0} \frac{\sin x}{e^{6x} - 1}[/m]
Следствие из 2 Замечательного предела:
[m]\lim \limits_{t \to 0} \frac{e^{t} - 1}{t} = 1[/m]
Поэтому:
[m]\lim \limits_{x \to 0} \frac{\sin x}{e^{6x} - 1} = \lim \limits_{x \to 0} \bigg (\frac{\sin x}{x} \cdot \frac{6x}{e^{6x} - 1} \cdot \frac{x}{6x} \bigg ) = 1 \cdot 1 \cdot \lim \limits_{x \to 0} \frac{x}{6x} = \frac{1}{6}[/m]
8) [m]\lim \limits_{x \to 0} \frac{\ln (6x + 1)}{arctg\ x}[/m]
Следствие из 1 Замечательного предела:
[m]\lim \limits_{t \to 0} \frac{arctg\ t}{t} = 1[/m]
Следствие из 2 Замечательного предела:
[m]\lim \limits_{t \to 0} \frac{\ln (t+1)}{t} = 1[/m]
Поэтому:
[m]\lim \limits_{x \to 0} \frac{\ln (6x + 1)}{arctg\ x} = \lim \limits_{x \to 0} \bigg ( \frac{x}{arctg\ x} \cdot \frac{\ln (6x+1)}{6x} \cdot \frac{6x}{x} \bigg ) = 1 \cdot 1 \cdot \lim \limits_{x \to 0} \frac{6x}{x} = 6[/m]