Задача 79932 Задание на фото. Найти экстремумы...
Условие
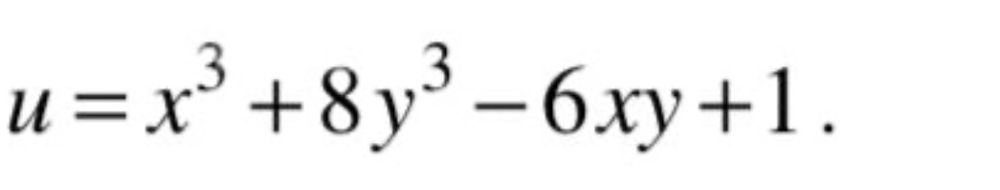
Решение
1) Необходимое условие экстремума:
Все производные 1 порядка должны быть равны 0.
[m]\large \frac{du}{dx} = 3x^2 - 6y = 0[/m]
[m]\large \frac{du}{dy} = 24y^2 - 6x = 0[/m]
Получили систему:
{ 3x^2 - 6y = 0
{ 24y^2 - 6x = 0
Делим 1 уравнение на 3, а 2 уравнение на 6:
{ x^2 - 2y = 0
{ 4y^2 - x = 0
Подставляем 2 уравнение в 1 уравнение:
{ x = 4y^2
{ 16y^4 - 2y = 0
2y(8y^3 - 1) = 0
2y(2y - 1)(4y^2 + 2y + 1) = 0
y1 = 0; x1 = 4y^2 = 4*0^2 = 0
y2 = 1/2; x2 = 4*(1/2)^2 = 4*1/4 = 1
Критические точки:
[b]A1(0; 0); A2(1; 1/2)[/b]
2) Достаточное условие экстремума:
[m]\large A = \frac{d^2u}{dx^2} = 6x[/m]
[m]\large B = \frac{d^2u}{dxdy} = -6[/m]
[m]\large C = \frac{d^2u}{dy^2} = 48y[/m]
В критических точках:
[m]A(0; 0) = 6 \cdot 0 = 0[/m]
[m]A(1; 1/2) = 6 \cdot 1 = 6 > 0[/m]
[m]C(0; 0) = 48 \cdot 0 = 0[/m]
[m]C(1; 1/2) = 48 \cdot \frac{1}{2} = 24 > 0[/m]
[m]D(0; 0) = AC - B^2 = 0 \cdot 0 - (-6)^2 = 36 > 0[/m]
[m]D(1; 1/2) = AC - B^2 = 6 \cdot 24 - (-6)^2 = 144 - 36 = 108 > 0[/m]
Правило для экстремумов функции двух переменных:
Если D > 0 и A > 0 - это минимум
Если D > 0 и A < 0 - это максимум
Во всех остальных случаях в критической точке экстремума нет.
В точке A1(0; 0) будет D = 36 > 0; A = 0 - экстремума нет.
В точке A2(1; 1/2) будет D = 108 > 0; A = 6 > 0 - это точка минимума.