Задача 79928 y=x^2, y=-3x+18, y=0 ...
Условие
Решение
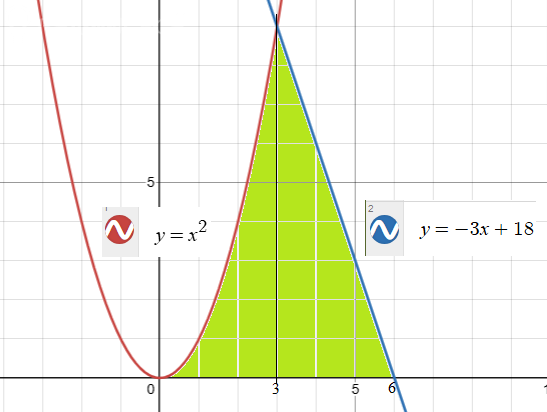
Фигура на рисунке закрашена зеленым цветом.
Чтобы найти пределы интегрирования, нужно приравнять функции:
1) x^2 = 0
[b]x1 = 0[/b]
2) x^2 = -3x + 18
x^2 + 3x - 18 = 0
(x + 6)(x - 3) = 0
x = -6 - не подходит
[b]x2 = 3[/b]
3) -3x + 18 = 0
3x = 18
[b]x3 = 6[/b]
Фигура состоит из двух криволинейных трапеций. Граница между ними x = 3
показана тонкой черной линией.
[m]S=\int \limits_0^3 x^2 dx + \int \limits_3^6 (-3x + 18) dx = \frac{x^3}{3} \bigg |_0^3 + (- \frac{3x^2}{2} + 18x) \bigg |_3^6 =[/m]
[m]= \frac{3^3}{3} - \frac{0^3}{3} + (- \frac{3 \cdot 6^2}{2} + 18 \cdot 6) - (- \frac{3 \cdot 3^2}{2} + 18 \cdot 3) =[/m]
[m]= 9 - 0 - 54 + 108 + \frac{27}{2} - 54 = 9 + 13,5 = 22,5[/m]
Ответ: S = 22,5