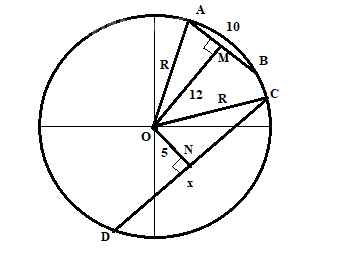
Задача 79879 Отрезки AB и CD являются хордами...

681f698f5fd3d26f525ef51c

5/10/2025 2:59:41 PM

Отрезки AB и CD являются хордами окружности найдите длину хорды CD если ab = 10 а расстояние от центра окружности до хорд ab и cd равны соответственно 12 и 5

626fab9a354ab65fb2f43abb

5/11/2025 8:13:26 AM

★

Смотрите рисунок.
Дано: AB = 10
OM ⊥ AB, OM = 12
ON ⊥ CD, ON = 5,
Найти: CD

Как известно, если радиус перпендикулярен хорде, то он делит хорду пополам.
AM = MB = 10/2 = 5
CN = ND = x/2
Из прямоугольного треугольника AOM по теореме Пифагора:
OA = sqrt(OM^2 + AM^2) = sqrt(12^2 + 5^2) = 13
(5, 12, 13) - это известная пифагорова тройка, можно не вычислять корень, а сразу написать ответ.
Радиус окружности остается один и тем же:
R = OA = OC.
Теперь из прямоугольного треугольника CON опять по теореме Пифагора:
CN = sqrt(OC^2 - ON^2) = sqrt(13^2 - 5^2) = 12
Но CN = ND
CD = x = 2*CN = 2*12 = 24

Ответ: 24