Задача 79826 Найти математическое ожидание...
Условие
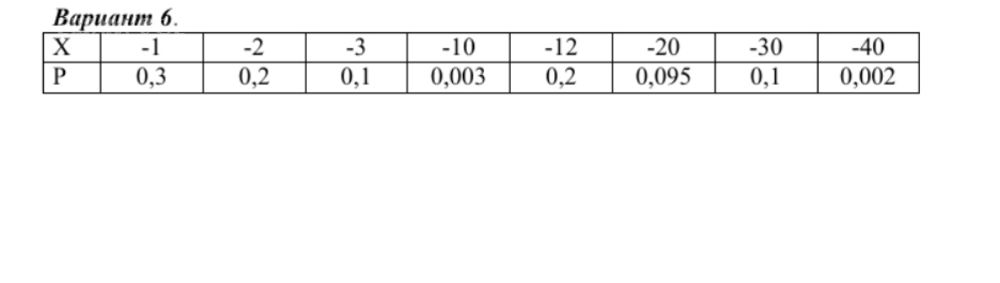
Решение
[m]M(X) = \sum \limits_{i=1}^{n} x_{i} \cdot p_{i}[/m]
M(X) = -1*0,3 - 2*0,2 - 3*0,1 - 10*0,003 - 12*0,2 - 20*0,095 - 30*0,1 - 40*0,002
M(X) = -0,3 - 0,4 - 0,3 - 0,03 - 2,4 - 1,9 - 3 - 0,08 = -8,41
Квадрат математического ожидания:
(M(X))^2 = (-8,41)^2 = 70,7281
Квадратичное математическое ожидание:
[m]M(X^2) = \sum \limits_{i=1}^{n} x_{i}^2 \cdot p_{i}[/m]
M(X^2) = 1^2*0,3 + 2^2*0,2 + 3^2*0,1 + 10^2*0,003 + 12^2*0,2 + 30^2*0,1 + 40^2*0,002
M(X^2) = 1*0,3 + 4*0,2 + 9*0,1 + 100*0,003 + 144*0,2 + 900*0,1 + 1600*0,002
M(X^2) = 0,3 + 0,8 + 0,9 + 0,3 + 28,8 + 90 + 3,2 = 124,3
Дисперсия:
D(X) = M(X^2) - (M(X))^2 = 124,3 - 70,7281 = 53,5719
Среднее квадратичное отклонение:
σ(X) = sqrt(D(X)) = sqrt(53,5719) ≈ 7,32