Задача 79818 Нужно решить задачу 12...
Условие
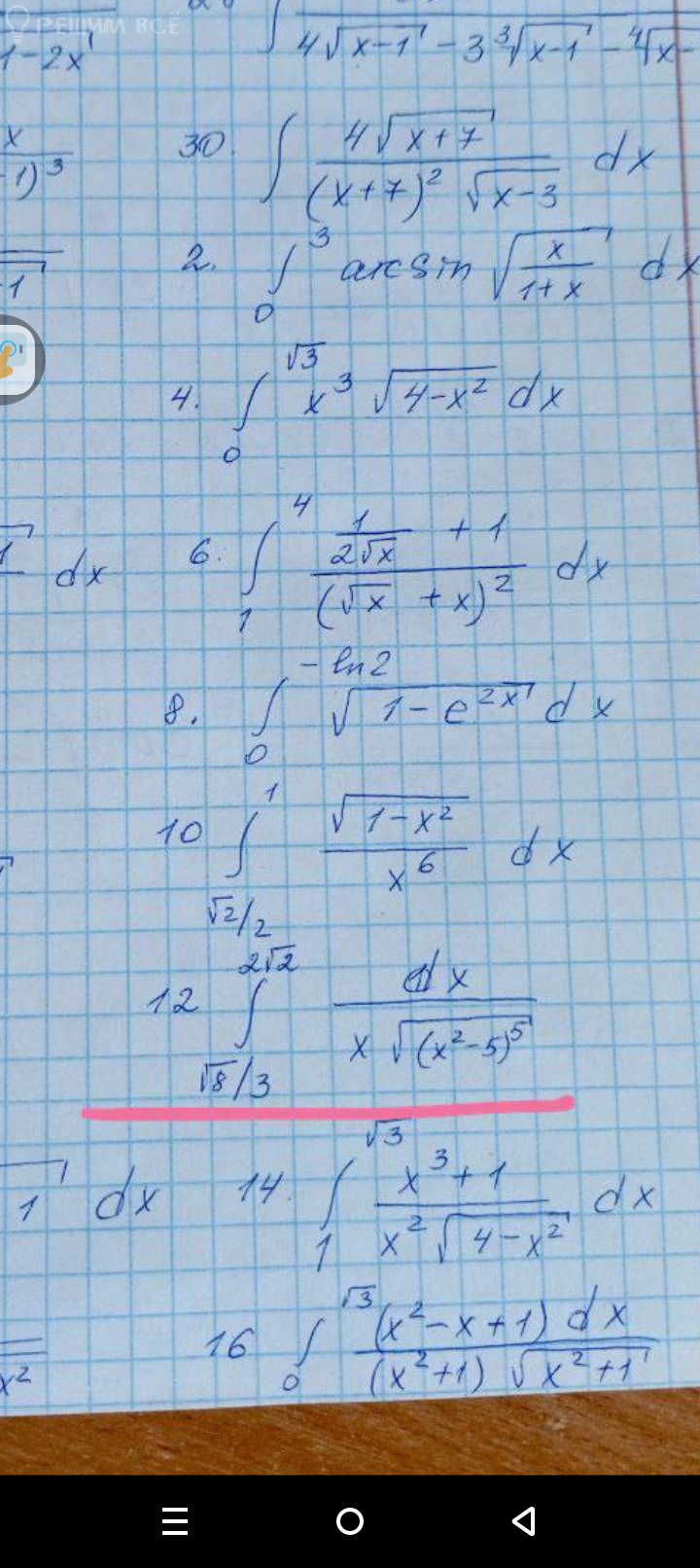
Решение
[m]\int \limits_{\sqrt{8}/3}^{\sqrt{8}} \frac{dx}{x \cdot \sqrt{(x^2-5)^5}}[/m]
Сначала решаем неопределенный интеграл, потом будем подставлять пределы:
[m]\int \frac{dx}{x \cdot \sqrt{(x^2-5)^5}[/m]
Замена u = x^2-5, du = 2x dx, dx/x = 1/2*du/x^2 = 1/2*du/(u+5)
[m]\int \frac{1}{2} \cdot \frac{du}{(u+5) \cdot u^{5/2}} = \frac{1}{2} \cdot \int \frac{du}{u^{7/2}+5u^{5/2}}[/m]
Новая замена v = u^(1/2) = sqrt(u); u = v^2; du = 2v dv
[m]\frac{1}{2} \cdot \int \frac{2v dv}{v^7+5v^5} = \frac{1}{2} \cdot 2 \int \frac{dv}{v^6+5v^4} = \int \frac{dv}{v^4(v^2+5)}[/m]
Метод неопределенных коэффициентов:
[m]\frac{1}{v^4(v^2+5)} = \frac{Av+B}{v^2+5} + \frac{C}{v}+ \frac{D}{v^2}+ \frac{E}{v^3}+ \frac{F}{v^4} =\frac{(Av+B)v^4 + Cv^3(v^2+5) + Dv^2(v^2+5) + Ev(v^2+5) + F(v^2+5)}{v^4(v^2+5)} =[/m]
[m]= \frac{(A+C)v^5 + (B+D)v^4 + (5C+E)v^3 + (5D+F)v^2 + 5Ev + 5F}{v^4(v^2+5)}[/m]
Составляем систему по коэффициентам при степенях v:
{ A + C = 0
{ B + D = 0
{ 5C + E = 0
{ 5D + F = 0
{ 5E = 0
{ 5F = 1
Решение этой системы:
{ F = 1/5
{ E = 0
{ D = -1/25
{ C = 0
{ B = 1/25
{ A = 0
Получаем разложение на дроби:
[m]\frac{1}{v^4(v^2+5)} = \frac{1}{25} \frac{1}{v^2+5} - \frac{1}{25} \frac{1}{v^2} + \frac{1}{5} \frac{1}{v^4}[/m]
Подставляем в интеграл:
[m]\int (\frac{1}{25} \frac{1}{v^2+5} - \frac{1}{25} \frac{1}{v^2} + \frac{1}{5} \frac{1}{v^4}) dv = \frac{1}{25} \int \frac{dv}{v^2+5} - \frac{1}{25} \int \frac{dv}{v^2} + \frac{1}{5} \int \frac{dv}{v^4} =[/m]
[m]= \frac{1}{25} \cdot \frac{1}{\sqrt{5}} \cdot arctg \frac{v}{\sqrt{5}} + \frac{1}{25} \cdot \frac{1}{v} - \frac{1}{5} \cdot \frac{1}{3v^3} = \frac{\sqrt{5}}{125} \cdot arctg \frac{v}{\sqrt{5}} + \frac{1}{25v} - \frac{1}{15v^3}[/m]
Обратная замена: v = sqrt(u)
[m]\frac{\sqrt{5}}{125} \cdot arctg \frac{v}{\sqrt{5}} + \frac{1}{25v} - \frac{1}{15v^3} = \frac{\sqrt{5}}{125} \cdot arctg \frac{\sqrt{u}}{\sqrt{5}} + \frac{1}{25\sqrt{u}} - \frac{1}{15\sqrt{u^3}}[/m]
Вторая обратная замена: u = x^2 - 5
[m]\frac{\sqrt{5}}{125} \cdot arctg \frac{\sqrt{u}}{\sqrt{5}} + \frac{1}{25\sqrt{u}} - \frac{1}{15\sqrt{u^3}} = \frac{\sqrt{5}}{125} \cdot arctg \frac{\sqrt{x^2 - 5}}{\sqrt{5}} + \frac{1}{25\sqrt{x^2 - 5}} - \frac{1}{15\sqrt{(x^2 - 5)^3}}[/m]
Подставляем пределы интегрирования:
[m]\int \limits_{\sqrt{8}/3}^{\sqrt{8}} \frac{dx}{x \cdot \sqrt{(x^2-5)^5}} = \frac{\sqrt{5}}{125} \cdot arctg \frac{\sqrt{x^2 - 5}}{\sqrt{5}} |_{\sqrt{8}/3}^{\sqrt{8}} + \frac{1}{25\sqrt{x^2 - 5}} |_{\sqrt{8}/3}^{\sqrt{8}} - \frac{1}{15\sqrt{(x^2 - 5)^3}} |_{\sqrt{8}/3}^{\sqrt{8}}[/m]
Оказывается, внутри интервала находится точка разрыва: x0 = sqrt(5) ∈ [sqrt(8)/3; sqrt(8)]
Интеграл определен только для x > sqrt(5), а sqrt(8)/3 < sqrt(5)
Поэтому это несобственный интеграл, и он расходится.
Ответ: Интеграл расходится.