Задача 79813 Центр круга, вписанного в прямоугольную...

66f286c87e3eee7b6aef8ece

5/2/2025 9:45:30 AM

Центр круга, вписанного в прямоугольную трапецию, удален от
концов ее боковой стороны соответственно на 75 и 100 см. Вычислить площадь трапеции. Решить с рисунком

626fab9a354ab65fb2f43abb

5/2/2025 8:34:29 PM

★

Смотрите рисунок.
Свойство трапеции, в которую можно вписать окружность:
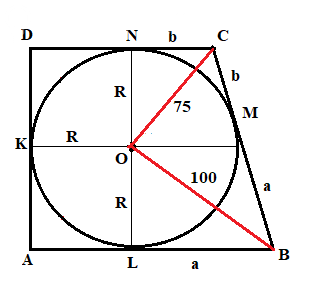
AK = AL; BL = BM; CN = CM; DK = DN
В нашем случае некоторые отрезки ещё и равны радиусу окружности:
OK = ON = AL = AK = KD = DN = R
Обозначим LB = a, NC = b, тогда:
AB = R + a; CD = R + b
По теореме Пифагора для треугольников ONC и OLB:
{ R^2 + b^2 = 75^2
{ R^2 + a^2 = 100^2
Но что с этим дальше делать - совершенно непонятно!
Есть подозрение, что треугольник OBC - тоже прямоугольный.
Но как это доказать, я не знаю. Тогда:
BC^2 = OC^2 + OB^2 = 75^2 + 100^2 = 5625 + 10000 = 15625 = 125^2
BC = a + b = 125
Тогда получаем систему:
{ R^2 + b^2 = 5625
{ R^2 + a^2 = 10000
{ b = 125 - a
Решаем подстановкой:
{ R^2 = 5625 - (125 - a)^2
{ R^2 = 10000 - a^2
5625 - 15625 + 250a - a^2 = 10000 - a^2
250a - 10000 = 10000
250a = 20000
a = 80
b = 125 - a = 125 - 80 = 45
R^2 = 10000 - a^2 = 10000 - 80^2 = 10000 - 6400 = 3600
R = 60
Основания трапеции:
AB = R + a = 60 + 80 = 140
CD = R + b = 60 + 45 = 105
Высота: h = AD = 2R = 2*60 = 120
Площадь трапеции:
S = (AB + CD)*h/2 = (140 + 105)*120/2 = 245*60 = 14700 см^2