Задача 79802 Стороны треугольника относятся между...

66f286c87e3eee7b6aef8ece

4/28/2025 5:21:14 PM

Стороны треугольника относятся между собой, как 4:13:15, а площадь
равно 24 см2. Найти стороны треугольника. Решение подать вместе с рисунокм

626fab9a354ab65fb2f43abb

4/28/2025 7:36:51 PM

★

Вот рисунок. Я нарисовал отрезок AB = 15 и две дуги окружностей, радиусами 13 и 4.
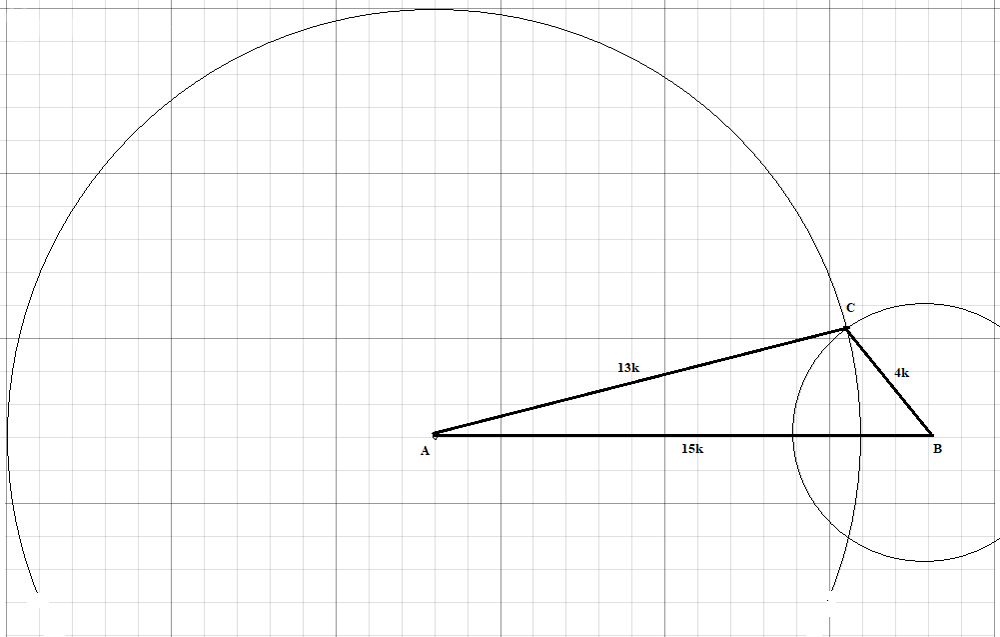
Центы этих окружностей находятся на концах отрезка AB.
Дуги пересеклись в какой-то точке и получился треугольник ABC со сторонами 4, 13, 15.
Обозначил их BC = 4k, AC = 13k, AB = 15k.
Площадь треугольника можно посчитать по формуле Герона:
[m]S = \sqrt{p(p-a)(p-b)(p-c)}[/m]
Где a, b, c - стороны треугольника, p = (a+b+c)/2 - полупериметр.
В нашем случае a = 4k, b = 13k, c = 15k, p = (4k+13k+15k)/2 = 16k
p - a = 16k - 4k = 12k, p - b = 16k - 13k = 3k; p - c = 16k - 15k = k
[m]S = \sqrt{16k \cdot 12k \cdot 3k \cdot k} = \sqrt{16 \cdot 3 \cdot 4 \cdot 3 \cdot k^4} = 4 \cdot 3 \cdot 2 \cdot k^2= 24k^2[/m]
По условию площадь равна 24 см^2, значит:
[m]24 = 24k^2[/m]
[m]k^2 = 1[/m]
[m]k = 1[/m]
Значит, стороны как раз и равны 4 см, 13 см и 15 см.